XIN队算法
注:名称由莫队算法改编而来
从luogu搬过来了。。。
\(newly\;upd:2021.7.8\)
\(newly\;upd:2021.6.6\)
OI至高算法,只要XIN队算法打满,保证所有比赛 \(rk1\),碾爆标程,让对手望尘莫及。
请慎用
XIN队算法:
1.遇到不会做的题目不用慌,你要想到你还有XIN队算法,仔细读题,理解题目意义,然后开始准备写XIN队算法。
2.这时候,你可以潇洒地敲出:
void xin_team()
然后开始暴搜
XIN队算法框架:
void xin_team(参数)
{
if(边界) return;
for(register int i=1;i<=n;++i)
if(条件1)
{
状态转移
xin_team(参数);
状态回溯
}
}
但是,对于不同的题目, void xin_team 并不能解决所有的题目,那该怎么办呢???
对于很多不能用XIN队\(1\)号算法的,大多数可以使用XIN队\(2\)号算法:next_permutation(a+1,a+n+1); 大法
框架:
void xin_team2
{
do
{
答案记录
}while(next_permutation(a+1,a+n+1));
}
非常完美
但是,由于XIN队算法时间复杂度 只有 \(\mathcal O(2^n)\)或者是\(\mathcal O(n!)\),所以我们提出优化:
优化XIN队算法:
非常不建议使用
框架:
srand((unsigned)time(0));
do
{
random_shuffle(a+1,a+n+1);
答案记录
}while(next_permutation(a+1,a+n+1));
复杂度:
还附加超大常数
XIN队算法升级:二维XIN队
有很多很多的题目无法用普通的\(XIN\)队算法解决,这时候我们就需要\(XIN\)队算法升级版:\(\color{red}\huge_{\text{二维XIN队}}\)
二维\(XIN\)队对于代码能力的提升是显而易见的,然而对复杂度的提升更是显而易见的,二维\(XIN\)队算法框架:
比方说:
使用此算法,轻松 \(30pts\)
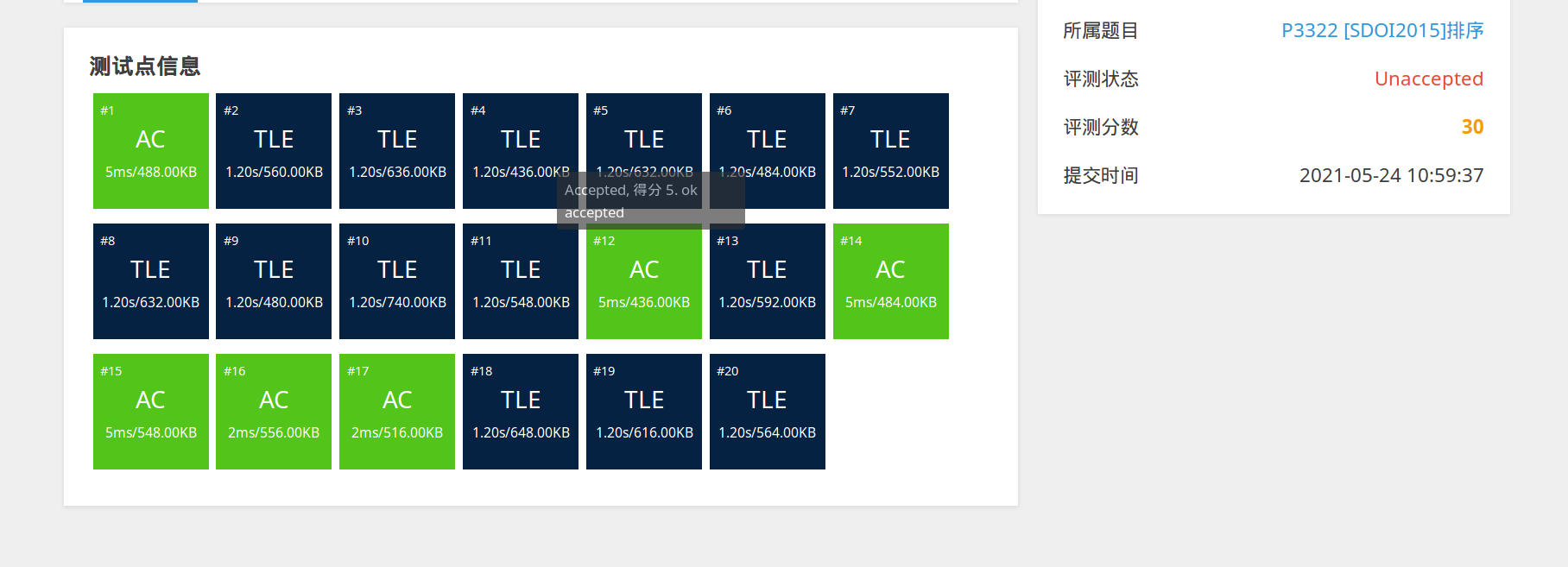
void xin_team2(int x,int now)
{
if(边界)
{
xin_team2(x,now);
记录
return ;
}
for(register int i=1;i<=n;++i)
{
记录状态
xin_team(x,now+1);
回溯状态
}
}
void xin_team1(int x,int now)
{
if(边界)
{
xin_team2(x,now);
记录
return ;
}
for(register int i=1;i<=n;++i)
{
记录状态
xin_team(x,now+1);
回溯状态
}
}
复杂度:
并且只能说是大概
我们发现,对于一般的题目,大多是 \(dp\) 解决,然而纯粹运用上述方法只能拿到部分分数,甚至全部 \(TLE\) 所以,记忆化 \(XIN\) 队算法应运而生。
对于优秀的记忆化 \(XIN\) 算法,想要什么状态就去找什么状态,然后就可以实现飞一般的提升。。。
包准快
使用记忆化 \(XIN\) 队算法,\(NOI\)包准不打铁!
比方说这个题: \(NOI2020\)美食家
使用 \(XIN\) 队算法,轻轻松松 \(40pts\)

框架:
void xin_team(int i,int j)
{
if(f[i][j]) return f[i][j];
for(k ...)
xin_team(k,~);
return f[i][j];
}
算法的时间复杂度就是:
\(num\)为状态,复杂度总体海星。。。
然而:
\(\color{red} \huge{\text{方程推不出}}\)
\(\color{green} \huge{\text{亲人两行泪}}\)
\(XIN\) 优化分块预处理
一个月没更了,这次在刷题的时候发现了最新的 \(XIN\) 队算法应用
这是在写蒲公英的时候发现的。

做了好长时间,中途还跑去做树链去了。


时间相差的确实长了一些。。。
在用分块解决这个问题的时候。
发现狂 \(T\) 不止。
但是。
不知道为什么在其他的 \(OJ\) 上都可以过掉
只不过就是很慢。
但是在学校的 \(OJ\) 上最多只有 \(70pts\)。
好评测机
然而并不敢找老师去开大时限
所以我只能优化暴力。。。
然后。
我发现在预处理 \(p_{i,j}\) 的时候,时间差的很多很多。
然而如果用 \(query\) 函数而不是暴力去搞就会错。。。
因为有些需要的状态还没有附上值但是接下来处理需要用到。。。
所以我集中生智
发现了 \(XIN\) 队优化分块预处理法
我都没想到 \(XIN\) 队算法还有优化别的东西的一天
主要思想就是 缺啥找啥
然后状态就有了。。。
双指针突然不香了 \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) --摇摆兵
然后飞快

void xin_team(int x,int y)
{
if(p[x][y]) return;
if(abs(y - x) <= 2) {p[y][x] = p[x][y] = query(l[x],r[y],0); return;}
xin_team(x+1,y-1);
p[x][y] = p[y][x] = query(l[x],r[y],0);
}
\(\color{red}{\huge{\uparrow \text{精华}}}\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\huge{record}\)

