『笔记』二分图

时间：2024-01-28 17:37:30

定义

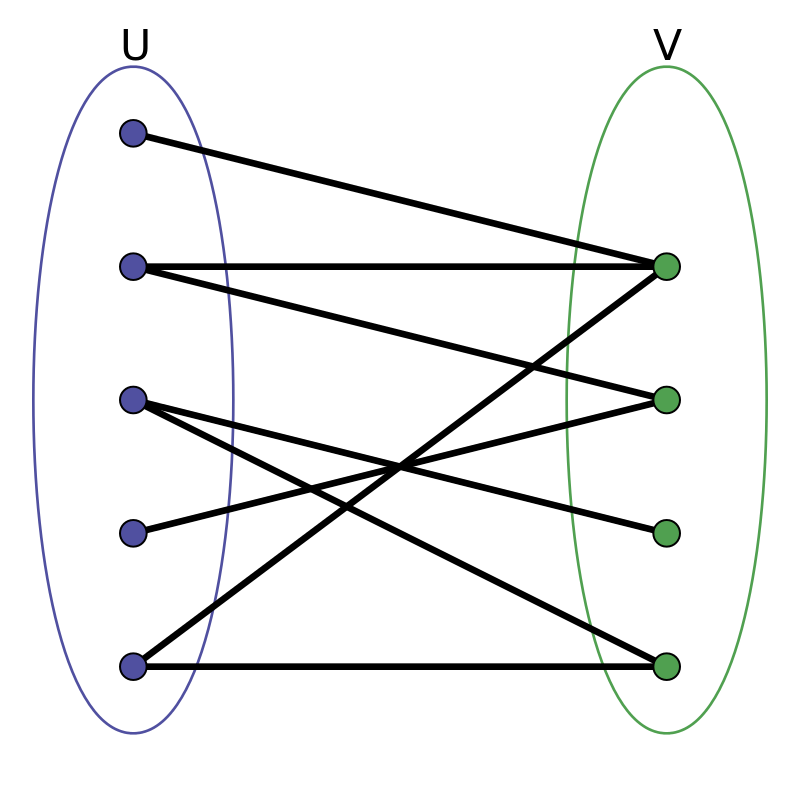
如果一张无向图的 \(N\) 个节点（ \(N \geq 2\) ），可以分成 \(U\) ， \(V\) 两个非空集合，其中 \(U \cap V = \Phi\) ，并且在同一集合内的点之间都没有边相连，那么称这张无向图为一张二分图。

\(U\) ， \(V\) 分别为二分图的左部和右部。

顶点集 \(U\) ， \(V\) 被称为是图的两个部分。

等价的 , 二分图 可以被定义成 图中所有的环都有偶数个顶点。

图片来自@Lucky Block

二分图判定

一张无向图是二分图，当且仅当图中不存在奇环。

证明

如果某个图是二分图，那么它至少有两个结点，且所有回路的长度均为偶数，任何无回路的图均是二分图。

一旦添加一条边后图中出现了回路，且长度一定为奇数，则该图就不再是二分图。

思想

根据上述定理，可以用染色法进行二分图判定。

用黑白两种颜色标记图中的节点，当一个节点被标记后，它的所有相邻节点应该被标记成与它相反的颜色。每个点只标记一次。

若标记过程中产生冲突，则说明存在奇环。

二分图染色一般基于 \(DFS\) 。

时间复杂度为 \(O ( N + M )\) 。

实现

/*

By 《算法竞赛进阶指南》

*/
void dfs(int x, int col)
{
    赋值 v[x] ← col;
    对于与 x 相连的每条无向边(x, y) if (v[y] = 0)
        dfs(y, 3 - col) else if (v[y] = col)
    {
        不是二分图;
        return;
    }
}

主函数中
{
    for (i = 1 → N)
        if (v[i] = 0)
            dfs(i, 1);
    判定无向图是二分图;
}

二分图匹配

云：

“任意两条边都没有公共端点”的边的集合被称为图的一组。

学长云：

给定一张图 \(G\) , 在 \(G\) 的一子图 \(M\) 中 , \(M\) 的边集中的任意两条边都没有共同的端点 , 则称 \(M\) 是一个匹配。

by @Lucky Block

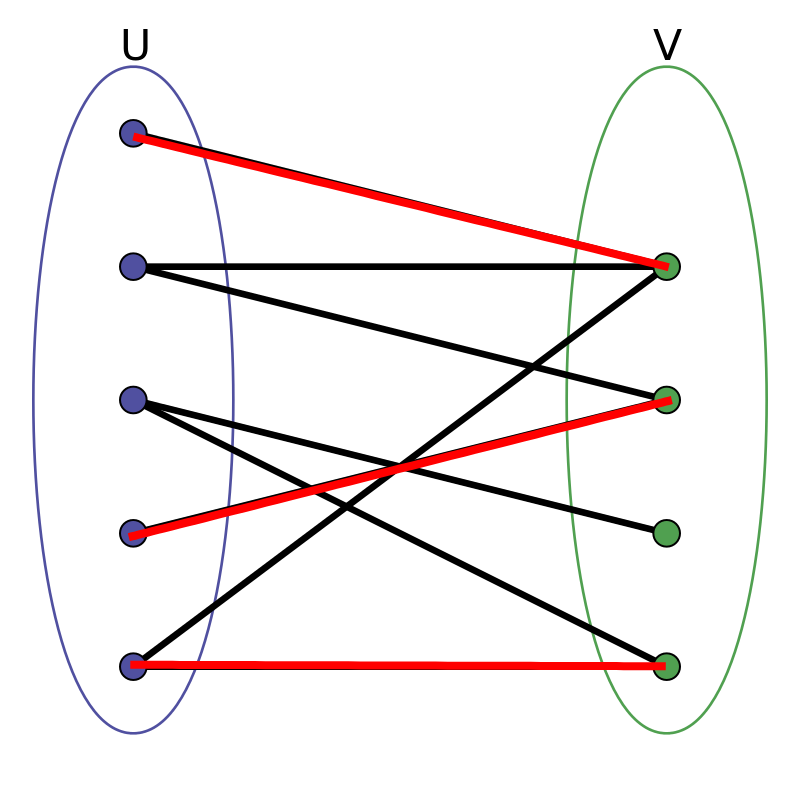
图片来自@Lucky Block

上图中的选择方案即为原图的一种匹配。

二分图最大匹配

云：

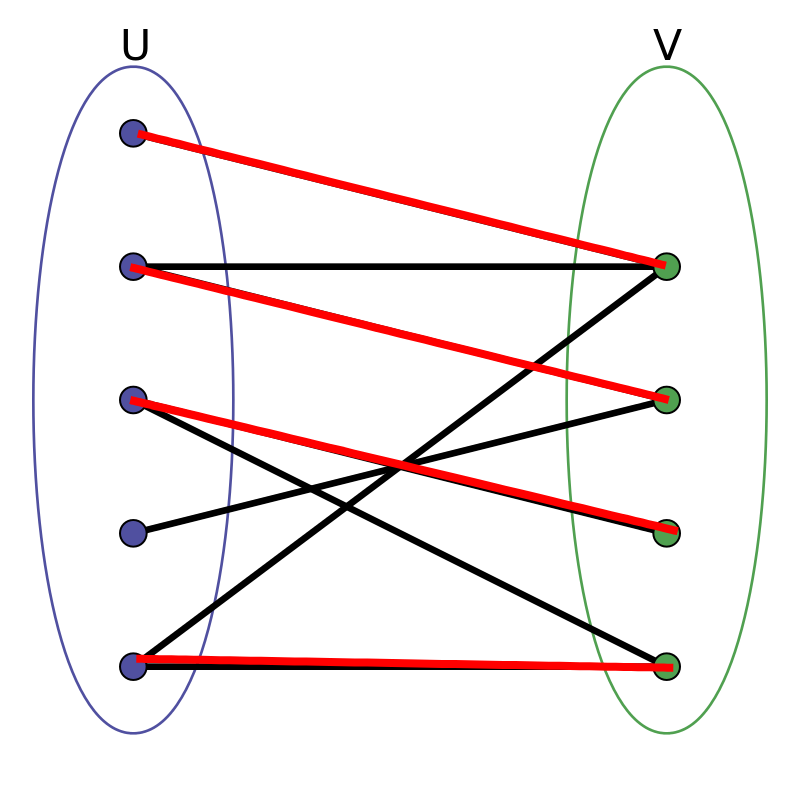
在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。

学长又云：

给定一张图 \(G\) , 其中边数最多的匹配 , 即该图的最大匹配。

@图片来自@Lucky Block

匈牙利算法（增广路算法）

核心

对于一匹配 \(M\) ,增广路径是指从 \(M\) 中未使用的顶点开始 , 并从 \(M\) 中未使用的顶点结束的交替路径 。

可以证明 , 一个匹配是最大匹配 , 当且仅当它没有任何增广路经。

即寻找增广路径 , 它是一种用 增广路径 求 二分图最大匹配的算法。

  1. 设 \(S=\Phi\) ，即所有边都是非匹配边。

  2. 寻找增广路 \(path\) ，把路径上所有边的匹配状态取反，得到一个更大的匹配 \(S'\) 。

  3. 重复第 \(2\) 步，知道图中不存在增广路。

观摩学长给出的一个样例

@图片来自@Lucky Block

  • 对 \(Yugari\) 进行匹配 :

    其直接连接点 \(Reimu\) 未被匹配 , 则将 \(Yugari\) 与 \(Reimu\) 进行匹配

  • 对 \(Marisa\) 进行匹配 :

    其直接连接点 \(Patchouli\) 未被匹配 , 则将 \(Marisa\) 与 \(Patchouli\) 进行匹配

  • 对 \(Suika\) 进行匹配 :

    其直接连接点 \(Reimu\) 被匹配 , 检查 \(Reimu\) 的匹配点 \(Yugari\) 能否寻找到其他匹配点

    • \(Yugari\) 可与 \(Yuyuko\) 进行匹配 , 则将 \(Yugari\) 与 \(Yuyuko\) 进行匹配

      由于\(Yugari\) 匹配对象改变 , \(Reimu\) 未被匹配 , 则将 \(Suika\) 与 \(Reimu\) 进行匹配

  • 对 \(Aya\) 进行匹配 :

    其直接连接点 \(Reimu\) 被匹配 , 检查 \(Reimu\) 的匹配点 \(Suika\) 能否寻找到其他匹配点

    • \(Suika\) 无其他匹配点 , 不可将 \(Suika\) 与其他结点进行匹配

      由于 \(Suika\) 匹配对象不可改变 , \(Reimu\) 被匹配 , 则 \(Aya\) 无匹配点

则此二分图的一种最大匹配为 :

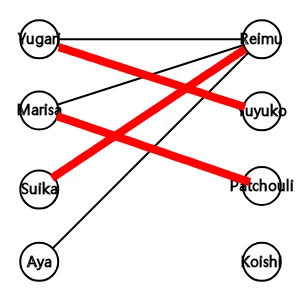
图片来自@Lucky Block

例题

P3386 【模板】二分图匹配

[P3386 【模板】二分图匹配](P3386 【模板】二分图匹配)

  • 如题，模板题是了。
/*

Name: P3386 【模板】二分图匹配

Solution: 二分图匹配
   

By Frather_

*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
/*=========================================快读*/
int read()
{
    int x = 0, f = 1;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-')
            f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = (x << 3) + (x << 1) + (c ^ 48);
        c = getchar();
    }
    return x * f;
}
/*=====================================定义变量*/
int n, m, t;

const int _ = 10010;

struct edge
{
    int from;
    int to;
    int nxt;
} e[_];
int cnt, head[_];
bool vis[_];
int mc[_];

int ans;
/*===================================自定义函数*/
void add(int from, int to)
{
    e[++cnt].from = from;
    e[cnt].to = to;
    e[cnt].nxt = head[from];
    head[from] = cnt;
}

bool check(int u_)
{
    for (int i = head[u_]; i; i = e[i].nxt)
        if (!vis[e[i].to])
        {
            vis[e[i].to] = true;
            if (!mc[e[i].to] || check(mc[e[i].to]))
            {
                mc[e[i].to] = u_;
                return true;
            }
        }
    return false;
}
/*=======================================主函数*/
int main()
{
    n = read();
    m = read();
    t = read();
    for (int i = 1; i <= t; i++)
    {
        int u = read();
        int v = read();
        add(u, v);
    }

    for (int i = 1; i <= n; i++)
    {
        memset(vis, false, sizeof(vis));
        if (check(i))
            ans++;
    }

    printf("%d\n", ans);
    return 0;
}

写在后面

鸣谢：

《算法竞赛进阶指南》

@Lucky Block

OI-wiki

百度百科

Luogu

相关文章