Life Winner Bo
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=5754
Description
Bo is a "Life Winner".He likes playing chessboard games with his girlfriend G.
The size of the chessboard is N×M.The top left corner is numbered(1,1) and the lower right corner is numberd (N,M).
For each game,Bo and G take turns moving a chesspiece(Bo first).At first,the chesspiece is located at (1,1).And the winner is the person who first moves the chesspiece to (N,M).At one point,if the chess can't be moved and it isn't located at (N,M),they end in a draw.
In general,the chesspiece can only be moved right or down.Formally,suppose it is located at (x,y),it can be moved to the next point (x′,y′) only if x′≥x and y′≥y.Also it can't be moved to the outside of chessboard.
Besides,There are four kinds of chess(They have movement rules respectively).
1.king.
2.rook(castle).
3.knight.
4.queen.
(The movement rule is as same as the chess.)
For each type of chess,you should find out that who will win the game if they both play in an optimal strategy.
Print the winner's name("B" or "G") or "D" if nobody wins the game.
Input
In the first line,there is a number T as a case number.
In the next T lines,there are three numbers type,N and M.
"type" means the kind of the chess.
T≤1000,2≤N,M≤1000,1≤type≤4
Output
For each question,print the answer.
Sample Input
4
1 5 5
2 5 5
3 5 5
4 5 5
Sample Output
G
G
D
B
Source
2016 Multi-University Training Contest 3
##题意:
给出N*M的棋盘和棋子的类型,两人以最优策略轮流走.
棋子初始时在(1,1), 先走到(N,M)者获胜.(只能往右下角方向移动)
问对于给定的情形先手胜、败、平.
##题解:
对于每个棋盘只有一个棋子,那么直接分析每个位置的必胜/必败态即可,对于最大的棋盘(1000*1000)打一次表即可.
(1000,1000)为必败态,从右下角往左上角逐个分析每点的状态:
可以到必败态的一定是必胜态; 只能到必胜态的一定是必败态.
1. king:可走到周围的8个格子.
当前位置(i,j)的状态由(i+1,j) (i,j+1) (i+1,j+1)确定.
2. rook:可以横着竖着走任意个格子.
简单推理可得只有i==j时必败,其余必胜.
3. knight:走"L"型路线.
当前位置(i,j)的状态由(i+2,j+1) (i+1,j+2)确定.
不同的是,题目要求不能移动且没有到右下角时为平手,那么只有knight可能出现平手,即走到边界时不能再移动.
对于当前位置,如果能走到必败态,那么一定是必胜态;若不能走到必败态,那么如果能走到平局位置,则一定是平局;
4. queen:横竖斜走任意格子.
对于每个必败态,将可到达的横竖斜格子全部置成必胜态.
(下面代码之所以跑了两遍,是因为第一次我把没有置1的位置全部置0,但是没有用这个0的位置去更新其他点,导致WA).
5. 这里提供样例(5*5)的四种棋子在各个位置的必胜必败态(1必胜 0必败 2平手), 供大家调错.
king:
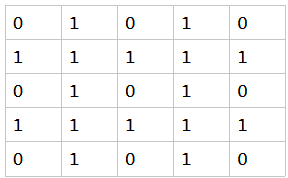
rook:
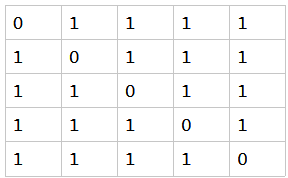
knight:
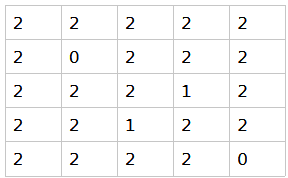
queen:
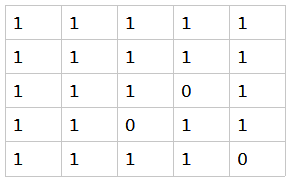
##代码:
``` cpp
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define LL long long
#define eps 1e-8
#define maxn 1010
#define mod 100000007
#define inf 0x3f3f3f3f
#define IN freopen("in.txt","r",stdin);
using namespace std;
int king[maxn][maxn];
int rook[maxn][maxn];
int knight[maxn][maxn];
int queen[maxn][maxn];
bool is_ok(int x, int y) {
return x>=1 && y>=1 && x<=1000 && y<=1000;
}
int main(int argc, char const *argv[])
{
//IN;
memset(king, -1, sizeof(king));
memset(rook, -1, sizeof(rook));
memset(knight, -1, sizeof(knight));
memset(queen, -1, sizeof(queen));
king[1000][1000] = 0;
rook[1000][1000] = 0;
knight[1000][1000] = 0;
queen[1000][1000] = 0;
for(int i=1000; i>=1; i--) {
for(int j=1000; j>=1; j--) {
if(king[i][j] != -1) continue;
if(is_ok(i+1,j) && !king[i+1][j]) {
king[i][j] = 1; continue;
}
if(is_ok(i,j+1) && !king[i][j+1]) {
king[i][j] = 1; continue;
}
if(is_ok(i+1,j+1) && !king[i+1][j+1]) {
king[i][j] = 1; continue;
}
king[i][j] = 0;
}
}
for(int i=1000; i>=1; i--) {
for(int j=1000; j>=1; j--) {
if(i==j) rook[i][j] = 0;
else rook[i][j] = 1;
}
}
for(int i=1000; i>=1; i--) {
for(int j=1000; j>=1; j--) {
if(knight[i][j] != -1) continue;
if(!is_ok(i+2,j+1) && !is_ok(i+1,j+2)) {
knight[i][j] = 2;
continue;
}
if(is_ok(i+2,j+1) && !knight[i+2][j+1]) {
knight[i][j] = 1; continue;
}
if(is_ok(i+1,j+2) && !knight[i+1][j+2]) {
knight[i][j] = 1; continue;
}
if(is_ok(i+2,j+1) && knight[i+2][j+1]==2) {
knight[i][j] = 2; continue;
}
if(is_ok(i+1,j+2) && knight[i+1][j+2]==2) {
knight[i][j] = 2; continue;
}
knight[i][j] = 0;
}
}
for(int i=1000; i>=1; i--) {
for(int j=1000; j>=1; j--) {
if(queen[i][j] != -1) {
if(queen[i][j] == 0) {
for(int k=1; k<=1000; k++) {
if(is_ok(i-k,j-k)) queen[i-k][j-k] = 1;
else break;
}
for(int k=1; k<=1000; k++) {
if(is_ok(i,j-k)) queen[i][j-k] = 1;
else break;
}
for(int k=1; k<=1000; k++) {
if(is_ok(i-k,j)) queen[i-k][j] = 1;
else break;
}
}
continue;
}
queen[i][j] = 0;
}
}
for(int i=1000; i>=1; i--) {
for(int j=1000; j>=1; j--) {
if(queen[i][j] != -1) {
if(queen[i][j] == 0) {
for(int k=1; k<=1000; k++) {
if(is_ok(i-k,j-k)) queen[i-k][j-k] = 1;
else break;
}
for(int k=1; k<=1000; k++) {
if(is_ok(i,j-k)) queen[i][j-k] = 1;
else break;
}
for(int k=1; k<=1000; k++) {
if(is_ok(i-k,j)) queen[i-k][j] = 1;
else break;
}
}
continue;
}
}
}
int t; cin >> t;
while(t--)
{
int tp,n,m; scanf("%d %d %d", &tp,&n,&m);
if(tp == 1) {
int ans = king[1000-n+1][1000-m+1];
if(ans) printf("B");
else printf("G");
}
if(tp == 2) {
int ans = rook[1000-n+1][1000-m+1];
if(ans) printf("B");
else printf("G");
}
if(tp == 3) {
int ans = knight[1000-n+1][1000-m+1];
if(ans == 1) printf("B");
else if(ans == 2) printf("D");
else printf("G");
}
if(tp == 4) {
int ans = queen[1000-n+1][1000-m+1];
if(ans) printf("B");
else printf("G");
}
printf("\n");
}
return 0;
}
