归并排序Python 实现

时间：2024-01-20 19:15:45
一、归并排序

-归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分合策略（将问题分(divide)成一些小的问题然后递归求解，而合的阶段则将分的阶段得到的各答案"修补"在一起，分久必合)。

归并排序Python 实现

 

1.2 一次归并

- 一次归并
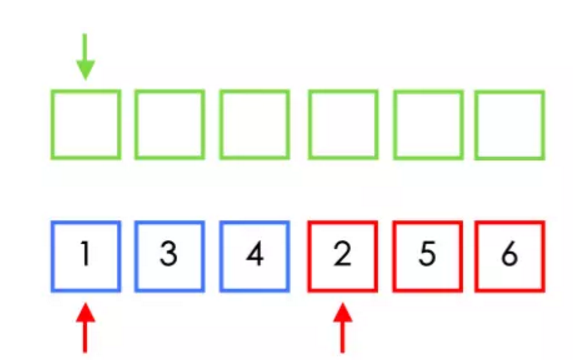
![](https://img2018.cnblogs.com/blog/1226829/201809/1226829-20180924192146754-191792692.png)

如图按照图中的一组数组被分成两半，蓝色和红色都是分别排好序了的

  • 然后按照中间分割区，选两个箭头一个指向左边最小，一个指向右边最小，将两个箭头对应的数比较，把较小的个放入上面的新列表

    归并排序Python 实现

  • 赋值完成后，将绿色标记自增1。左侧红色标记自增1。

    归并排序Python 实现

  • 然后继续比较两个数组红色标记处的元素。此时右侧数组元素小，所以将右侧数组标记处元素赋值给绿色数组的绿色标记处。

    归并排序Python 实现

  • 重复上面的步骤

    归并排序Python 实现

  • 最后得到结果

    归并排序Python 实现

这就称为一次归并排序

 

1.3 代码实现一次递归排序
def sort(lst, low, mid, high):

    i = low

    j = mid +1 # low ----> mid 代表了前面所有拍好序的一个组    mid 到 mid + 1 是乱序部分 mid+1 到最后又是另一个排好序的组

    lstm = []

    while i <= mid and j <= high:

        if lst[i] < lst[j]:  #比较两个指针指向的数的大小，把小的一个append到心列表， 并且谁放进去了，谁索引自增一

            lstm.append(lst[i])

            i += 1

        else:

            lstm.append(lst[j])

            j += 1

    # 出现 某一边，可能是左边可能是右边先排完了，将剩下的有序数全部处理添加到新列表

    while i <= mid:

        lstm.append(lst[i])

        i += 1

    while j <= high:

        lstm.append(lst[j])

        j += high

    lst[low: high+1] = lstm   #最后将拍好序新列表的，赋值回传入的列表的索引段

  • 这样一次归并排序就完成了

 

二、递归实现归并排序
  • 代码实现
def all_sort(lst, low, high):

    if low < high:

        mid = (low + high)//2  #1

        all_sort(lst, low, mid)  #2

        all_sort(lst, mid+1, high)  #3

        sort(lst, low, mid, high) #开始排序

  • 如图 #1处: mid = (low + high)//2 将列表一分为二， #2处递归前半段， #3出递归后半段。

    如：low=0, mid=2时还剩 0, 1, 2 三个数。下次计算mid=(low + high)//2 mid = 1, low=0. 表明只剩下两个数了，然后计算 (0 + 1)//2 = 0 这时low = mid = 0,继续传入#2就不会递归了，

     

    既然是两个数，中间一分开左右都是有序的,将两个数按照大小拍好，然后开始不断的把所有结果和到一起

  • 这就是归并排序的分解 与 合并

相关文章