机器学习之Logistic regression

Logistic regression (LR)是一种非常常用判别模型。在实际应用中使用非常广泛。为什么说LR是一种判别模型呢？它与生成式模型有什么区别呢？
一般来说，如果模型是直接对样本本身的分布建模 p(x|Ck) ，那么该模型就是生成式模型。反之，如果模型是对后验概率建模 p(Ck|x) ，那么该模型就是判别模型。
LR就是典型的概率模型，LR是针对两类问题进行分类。LR使用了sigmoid函数来对后验概率建模。

σ (z) = 1 1 + exp ( - z )

sigmoid函数具有如下性质：

\partial σ ( z ) \partial z = σ (z) (1 - σ (z))

而LR就是在线性模型基础上加上了一种sigmoid函数，

z y = p (C 1 | x) = = w T x + b σ (z)

假定有二分类问题，给定样本

(x1,t1),⋯,(xN,tN) 。其中

xn 为

D 维向量，

tn∈{0,1} 。注意到没有，

tn 是一个离散的

{0,1} 变量，和伯努利分布是一种的。那么：

p (t n | w, b) = y t n n (1 - y n) 1 - t n

那么对数似然为：

ln p (t | w, b) = \sum n = 1 N (t n ln y n + (1 - t n) ln (1 - y n))

令

E(w,b)=−lnp(t|w,b) ，最大化最大似然等价于最小化能力函数

E(w,b) ，

E(w,b) 对

w,b 求导为：

\partial E ( w , b ) \partial w \partial E ( w , b ) \partial b = = = - \sum n = 1 N (t n y n - 1 - t n 1 - y n) y n (1 - y n) x n \sum n = 1 N (y n - t n) x n \sum n = 1 N (y n - t n)

有了参数的导数，就可以利用梯度下降法来求解参数

w,b 。
目前为止，讨论的是二类问题。对于多类问题，也是类似的。将每一类的类别标签表示为one-hot的向量形式。而分类函数则为：

y k \partial y k \partial z j = = p (C k | W, b) = exp ( z k ) \sum K i = 1 exp ( z i ) y k (I k j - y j)

其中，

Ikj 表示单位矩阵。

W=[w1,w2,⋯,wK],b=[b1,b2,⋯,bK]T ，

zk 为：

z k = w T k x + b k

对于

K 类分类问题，给定样本

(x1,t1),⋯,(xN,tN)

p (t n | W, b) = \prod k = 1 K y t n k n k

对数似然为：

E = - ln p (T | W, b) = - \sum n = 1 N \sum k = 1 K t n k ln y n k

分别对

wj,bj 求导为：

\partial E \partial w j \partial E \partial b j = = = = \partial E \partial z j \partial z j \partial w j - \sum n = 1 N \sum k = 1 K t n k y n k y n k (I k j - y n j) x n \sum n = 1 N (y n j - t n j) x n \sum n = 1 N (y n j - t n j)

有了这个参数的导数就可以采用梯度下降法来求解参数。

w j b j = = w j - η \partial E \partial w j b j - η \partial E \partial b j

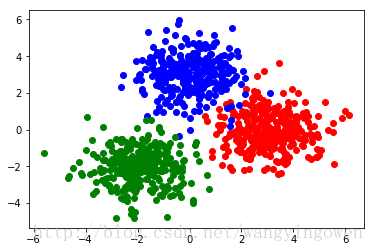
还是采用python来实现，首先用高斯函数生成三类样本

![这里写图片描述](https://img-blog.csdn.net/20171126214829183?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvd2FuZ3lpbmdvd2Vu/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)

代码

LR的例子：

from scipy.stats import multivariate_normal
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
N=1000;
N_train = 300;
X1=multivariate_normal.rvs(mean=[3,0],cov=[[1,0],[0,1]],size=N)#从均值为[0.3,0.5],方差为[[1,0.5],[0.5,1]]的二元高斯分布中生成10000个样本
T1=np.zeros([N,3]);
T1[:,0]=1.0;
X2=multivariate_normal.rvs(mean=[0,3],cov=[[1,0],[0,1]],size=N)
T2=np.zeros([N,3]);
T2[:,1]=1.0;
X3=multivariate_normal.rvs(mean=[-2,-2],cov=[[1,0],[0,1]],size=N)
T3=np.zeros([N,3]);
T3[:,2]=1.0;
#plt.plot(X1[:,0],X1[:,1],'or',X2[:,0],X2[:,1],'ob',X3[:,0],X3[:,1],'og')
Index1 = np.random.permutation(N)
TrainData1 = X1[Index1[0:N_train],:]
TestData1  = X1[Index1[N_train:N],:]
TrainLabel1 = T1[Index1[0:N_train],:]
TestLabel1 = T1[Index1[N_train:N],:]

Index2 = np.random.permutation(N)
TrainData2 = X2[Index2[0:N_train],:]
TestData2  = X2[Index2[N_train:N],:]
TrainLabel2 = T2[Index2[0:N_train],:]
TestLabel2 = T2[Index2[N_train:N],:]

Index3 = np.random.permutation(N)
TrainData3 = X3[Index3[0:N_train],:]
TestData3  = X3[Index3[N_train:N],:]
TrainLabel3 = T3[Index1[0:N_train],:]
TestLabel3  = T3[Index1[N_train:N],:]

#plt.plot(X1[:,0],X1[:,1],'or',X2[:,0],X2[:,1],'ob',X3[:,0],X3[:,1],'og')
plt.figure()
plt.plot(TrainData1[:,0],TrainData1[:,1],'or',TrainData2[:,0],TrainData2[:,1],'ob',TrainData3[:,0],TrainData3[:,1],'og')
TrainData=np.concatenate((TrainData1,TrainData2,TrainData3));
TrainLabel = np.concatenate((TrainLabel1,TrainLabel2,TrainLabel3));
N_t,d=TrainData.shape
index = np.random.permutation(N_t)
TrainData = TrainData[index,:]
TrainLabel = TrainLabel[index,:]
#plt.figure()
#plt.plot(TrainData[:,0],TrainData[:,1],'or')

#training process;
W = np.random.randn(2,3)
b = np.zeros([1,3])
eta = 0.01
IterNumber = 50000
Label_True = np.argmax(TrainLabel,axis=1)
#训练#
for i in range(IterNumber+1):
    Z = np.matmul(TrainData,W)+np.tile(b,[N_t,1])
    Y = np.exp(Z)
    M = np.sum(Y,axis=1)
    Y = np.divide(Y.transpose(),M).transpose() #输出标签#
    E = np.sum(np.multiply(TrainLabel,np.log(Y)))
    if np.remainder(i,100)==0:
        Index = np.argmax(Y,axis=1)
        D=(Index==Label_True)
        correct = np.sum(D)
        print('correct=',correct/N_t)
        print(E)
    YT=Y-TrainLabel;
    deltaW = np.matmul(TrainData.transpose(),YT) / N_t #W的梯度#
    deltaB = np.mean(YT,axis=0); #b的梯度#
    W = W-eta*deltaW;
    b = b-eta*deltaB;

#在测试集上的分类结果#
TestData=np.concatenate((TestData1,TestData2,TestData3));
TestLabel = np.concatenate((TestLabel1,TestLabel2,TestLabel3));
Label_True = np.argmax(TestLabel,axis=1)
N_test,dim=TestData.shape
Z = np.matmul(TestData,W)+np.tile(b,[N_test,1])
Y = np.exp(Z)
M = np.sum(Y,axis=1)
Y = np.divide(Y.transpose(),M).transpose() 
Index = np.argmax(Y,axis=1)
D=(Index==Label_True)
correct = np.sum(D)/N_test
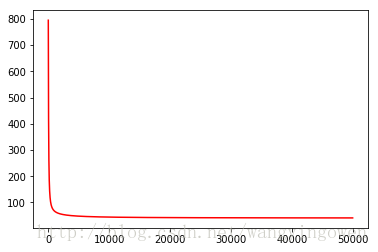
print('correct=',correct)

上面for循环过程就是训练过程。下图是能量函数的曲线，可以看出能量是下降的，说明训练过程是收敛的。

![收敛曲线](https://img-blog.csdn.net/20171126213952698?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvd2FuZ3lpbmdvd2Vu/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)

现在用tensorflow来实现下LR

LR的tensorflow实现（这里每次迭代都用到了所有样本，可以采用batch的方式）：

# -*- coding: utf-8 -*-
""" Created on Sat Nov 25 16:17:35 2017 @author: wangying """

from scipy.stats import multivariate_normal
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import tensorflow as tf

#生成模拟数据
N=1000;
N_train = 300;
X1=multivariate_normal.rvs(mean=[3,0],cov=[[1,0],[0,1]],size=N)#从均值为[0.3,0.5],方差为[[1,0.5],[0.5,1]]的二元高斯分布中生成10000个样本
T1=np.zeros([N,3]);
T1[:,0]=1.0;
X2=multivariate_normal.rvs(mean=[0,3],cov=[[1,0],[0,1]],size=N)
T2=np.zeros([N,3]);
T2[:,1]=1.0;
X3=multivariate_normal.rvs(mean=[-2,-2],cov=[[1,0],[0,1]],size=N)
T3=np.zeros([N,3]);
T3[:,2]=1.0;
#plt.plot(X1[:,0],X1[:,1],'or',X2[:,0],X2[:,1],'ob',X3[:,0],X3[:,1],'og')
Index1 = np.random.permutation(N)
TrainData1 = X1[Index1[0:N_train],:]
TestData1  = X1[Index1[N_train:N],:]
TrainLabel1 = T1[Index1[0:N_train],:]
TestLabel1 = T1[Index1[N_train:N],:]

Index2 = np.random.permutation(N)
TrainData2 = X2[Index2[0:N_train],:]
TestData2  = X2[Index2[N_train:N],:]
TrainLabel2 = T2[Index2[0:N_train],:]
TestLabel2 = T2[Index2[N_train:N],:]

Index3 = np.random.permutation(N)
TrainData3 = X3[Index3[0:N_train],:]
TestData3  = X3[Index3[N_train:N],:]
TrainLabel3 = T3[Index1[0:N_train],:]
TestLabel3  = T3[Index1[N_train:N],:]

#plt.plot(X1[:,0],X1[:,1],'or',X2[:,0],X2[:,1],'ob',X3[:,0],X3[:,1],'og')
plt.figure()
plt.plot(TrainData1[:,0],TrainData1[:,1],'or',TrainData2[:,0],TrainData2[:,1],'ob',TrainData3[:,0],TrainData3[:,1],'og')
TrainData=np.concatenate((TrainData1,TrainData2,TrainData3));
TrainLabel = np.concatenate((TrainLabel1,TrainLabel2,TrainLabel3));
N_t,d=TrainData.shape
index = np.random.permutation(N_t)
TrainData = TrainData[index,:]
TrainLabel = TrainLabel[index,:]
TestData=np.concatenate((TestData1,TestData2,TestData3));
TestLabel = np.concatenate((TestLabel1,TestLabel2,TestLabel3));

n_input_layer = 2 # 输入层

n_output_layer = 3       # 输出层
batch_size = 100
epochs=1000;
X = tf.placeholder('float',[None,2])
    #Y = tf.placeholder('float',[None,n_output_layer])
Y = tf.placeholder('float')
W = tf.Variable(tf.random_normal([2,3]),'W');
b = tf.Variable(tf.random_normal([3]));
def network(data):
    output = tf.add(tf.matmul(data,W),b);
    return output

predict = network(X)
cost_func = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=predict,labels=Y)) + 0.01*tf.nn.l2_loss(W)
tf.summary.scalar("loss", cost_func)
    #optimizer = tf.train.AdamOptimizer().minimize(cost_func)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost_func)
correct = tf.equal(tf.argmax(predict,1),tf.argmax(Y,1))
accuracy = tf.reduce_mean(tf.cast(correct,'float'))
def train_neural_network():
    #saver = tf.train.Saver()
    with tf.Session() as session:
        session.run(tf.global_variables_initializer())
        for epoch in range(epochs):
            epoch_loss= 0;
            _, epoch_loss = session.run([optimizer, cost_func], feed_dict={X:TrainData,Y:TrainLabel})
            print(epoch, ' : ', epoch_loss)

        print('准确率: ', accuracy.eval({X:TrainData, Y:TrainLabel}))
train_neural_network()

秒客网

机器学习之Logistic regression

机器学习之Logistic regression

代码

现在用tensorflow来实现下LR

相关文章