883. Projection Area of 3D Shapes

### 问题 NxN个格子中，用1x1x1的立方体堆叠，grid[i][j]表示坐标格上堆叠的立方体个数，求三视图面积。 > Input: [[1,2],[3,4]] Output: 17 Explanation: 见下图 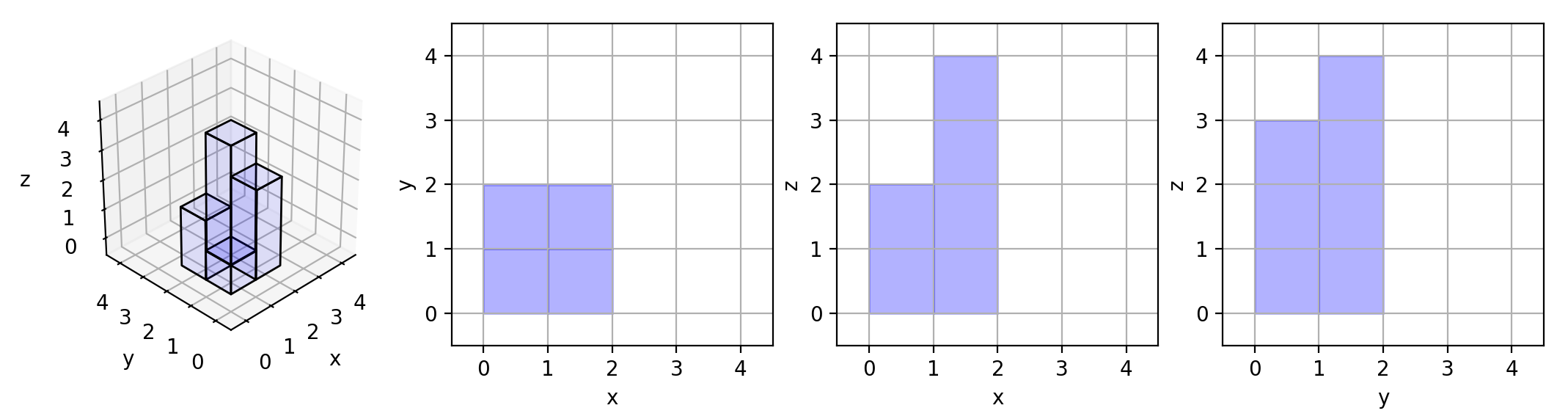 ### 思路 对于俯视图，只要一个格子有值，面积值就加1。 对于正视图（面朝x轴），对于某一个x，在y轴方向上拥有的最高grid值，表示，该x顺着y轴看过去看到的面积值。 对于侧视图（面朝y轴），对于某一个y，在x轴方向上拥有的最高grid值，表示，该y顺着y轴看过去看到的面积值。 把这些面积值加起来即可。 > 时间复杂度O(n^2，空间复杂度O(1) ### 代码 ```python class Solution(object): def projectionArea(self, grid): """ :type grid: List[List[int]] :rtype: int """ s = 0 n = len(grid) for i in range(n): best_row = 0 best_col = 0 for j in range(n): if(grid[i][j] > 0): s += 1 best_row = max(best_row, grid[i][j]) best_col = max(best_col, grid[j][i]) s += best_row + best_col return s ``` ### 类似题目 [892. Surface Area of 3D Shapes](https://www.cnblogs.com/liaohuiqiang/p/9829452.html)