[源码解析] 快手八卦 --- 机器学习分布式训练新思路(1)
0x00 摘要
“Bagua“ 是快手和苏黎世理工(ETH Zürich)联合开发的分布式训练框架。其专门针对分布式的场景设计特定的优化算法,实现算法和系统层面的联合优化,力图极致化分布式训练的效率。其特点是:
-
并行性能显著提高;
-
对网络环境更鲁棒;
-
“一键式”使用;
-
分布式通讯算法易拓展性;
-
可用于工业级场景大规模使用;
-
安全、故障易排查;
本文以:
- 快手官方公共号文章 快手八卦!突破 TensorFlow、PyTorch 并行瓶颈的开源分布式训练框架来了!
- “bagua"论文 https://arxiv.org/pdf/2107.01499.pdf
- “bagua"官方网站 https://tutorials.baguasys.com/
- “bagua" 演示文档
- 项目 GitHub 地址:https://github.com/BaguaSys/bagua
为基础来分析学习。本文学习“bagua"总体设计思路和负载均衡数据加载器。
0x01 设计思路
以下摘录于快手官方帖子 快手八卦!突破 TensorFlow、PyTorch 并行瓶颈的开源分布式训练框架来了! 和 ETH PPT,按照自己理解有调整。
1.1 如何通信
在数据并行之中,从单机单卡的训练到多机多卡训练的核心,是每个卡把自己的计算结果进行累加和传播,所以一个关键点是两个worker之间如何进行通信。

这个过程好比每个人把自己知道的信息传递给他人,然后又从其他人那里获取信息,最后完成全局的信息同步。如果把计算单元之间的信息同步类比为人与人之间的信息同步,那么社会实践经验告诉我们,“八卦”可能是消息传递最高效的模式。“八卦”消息传播具有去中心化、异步通讯、信息压缩的特点,这与 Bagua 里面实现的通讯算法刚好一一呼应。
1.2 通信模式分类
针对通信模式,有如下分类。

1.2.1 系统架构
按照系统架构来区分,是参数服务器和Allreduce。

下图是参数服务器和Allreduce范式的图例。
- 在参数服务器架构中,模型可以被分割成分片(shard)并分布到多个节点(我们称这些节点为 "参数服务器")。在训练阶段,worker定期从参数服务器获取模型,利用计算单元(如GPU)进行前向和后向传播,并将梯度推送给参数服务器,而参数服务器汇总梯度并更新参数。
- 在Allreduce范式之中,所有worker都与他们的邻居合作进行模型/梯度交换。现有的系统通常采用环形拓扑结构进行两阶段的交流:首先,范式将模型/梯度划分为n个块(其中n为节点数),并使用不同起点和终点的n个环来聚合n个块;其次,位于不同节点的每个块的聚合结果会在环内进行广播。

1.2.2 同步角度
从通信同步角度看可以分为同步或是异步(Synchronous or Asynchronous):
- 同步模式中,在每一次迭代过程中,所有工作节点都需要进行通信,并且下一步迭代必须等待当前迭代的通信完成才能开始。
- 反之,异步式分布算法 则不需要等待时间:当某个节点完成计算后就可直接传递本地梯度,进行模型更新。

1.2.3 通信拓扑
从通信拓扑角度看可以分成中心化或是去中心化(Centralized or Decentralized):
- 在中心化的通讯模式中,梯度或模型的同步过程需要所有的工作节点进行参与,因此,较高的网络延时往往会导致训练效率的降低。
- 去中心化的通信模式往往可以有效的解决上述问题:在该模式下,工作节点可以被连接成特定的拓扑结构(例如环),在通信过程中,每一个工作节点只与和它相邻的节点进行通信。

1.2.4 压缩
从通信压缩与否角度看,有完整精度模式或信息压缩模式(Full-Precision or Low-Precision)两种:
- 完整精度模式会使用与本地模型相同的 32 位浮点数(float32)进行传输。
- 另一方面,在通讯存在瓶颈的情况下,基于大量已有研究通过量化 (quantization) 或稀疏化 (sparsification) 等方法压缩梯度,再用压缩后的梯度更新参数。在很多场景下,可以达到和完整精度相同的精度,同时提升通讯效率。

1.3 挑战
快手在实现之中,遇到了三个挑战:
- 理论基础:通信模式需要有理论的支撑,需要严格在理论上证明通信是有效的,收敛的。
- 系统设计:现有分布式学习系统都无法满足所有的新的通信模式,所以需要设计新的系统结构,才能利用这种算法带来的优势。
- 参数服务器基本操作put/get,无法实现去中心化和误差补偿。
- Allreduce是全局性的,无法实现去中心化或者异步模式。
- 评测:需要在大规模真实场景下对各种算法进行评测。
1.4 Bagua 实现
1.4.1 分层
Bagua 具体分为三层:
- 算法层:在逻辑层基础之上,实现了具体算法,比如某一个算法是去中心化,压缩,异步的。
- 逻辑通信层:在物理通信层基础之上,实现了多种通信原语,比如去中心化,精度,同步等等,这些通信原语不是针对某一类算法特殊设计的,而对上层是统一的。
- 物理通信层:在此层集成了一些常见通信库,从而提供了基本的send,receive操作。

1.4.2 通信算法选项
针对通信模式分类,Bagua 相应将通信过程抽象成了如下的算法选项:
-
中心化或是去中心化(Centralized or Decentralized)。
-
同步或是异步(Synchronous or Asynchronous)。
-
完整精度模式或信息压缩模式(Full-Precision or Low-Precision)。
虽然为了提升通讯效率,Bagua 没有依照传统的方式同步所有计算节点的结果,甚至每次同步的信息还有偏差,但是得益于最新理论上的进展,这几种通讯策略以及他们的组合最终收敛解的正确性和效率仍然能得到充分保证,而且计算复杂度跟同步中心化和信息无损的方法相当,但是通讯效率更高。
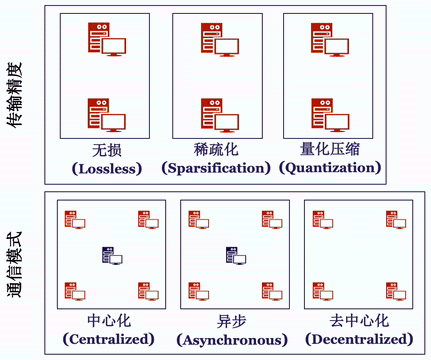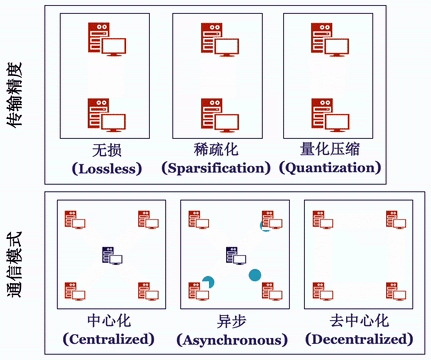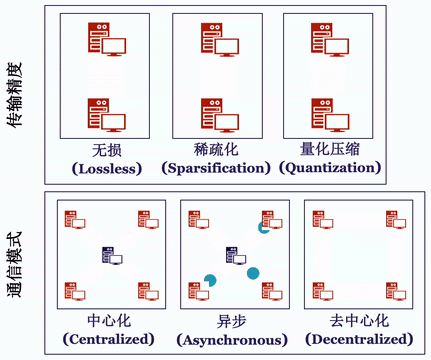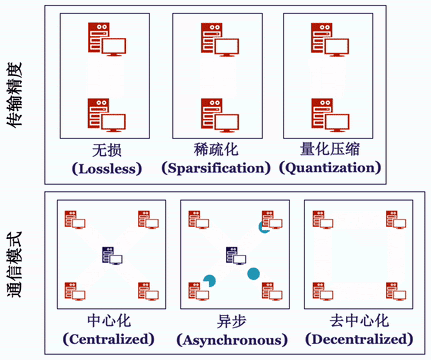
Bagua 提供了一套详尽的通信模式来支持用户在上述模式中任意选择组合,我们将这一分布式训练系统对于上述算法选项的支持情况总结在下表中:
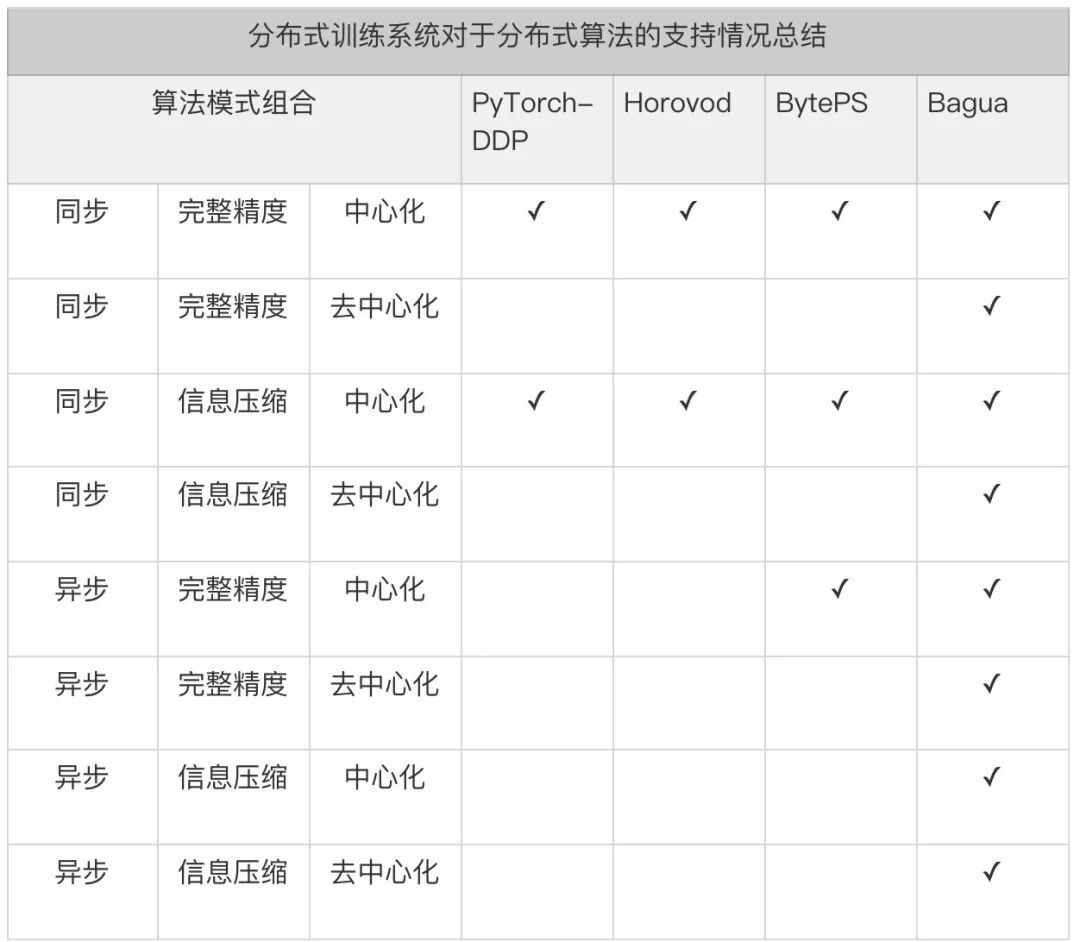
从表格中不难看出,现有框架的优化只是针对较为通用的算法(中心化同步完整精度),对于其他的算法组合,这些系统的支持非常有限。对于中心化同步进行信息压缩,这些系统往往只能支持较为简单的 float32->float16 压缩,相较而言,Bagua 则可以支持更为复杂的 ByteGrad,QAdam 等算法。对于其他的算法组合,现有的框架通常无法支持,而 Bagua 则可以*支持。
1.4.3 总体
BAGUA的核心是一个训练算法,由开发者使用BAGUA提供的通信原语和抽象概念来实现。算法将最终用户提供的神经网络作为输入,并为其配备一个特定于算法的通信功能。具体来说,算法的开发者会在执行的不同阶段将这个通信功能注册为钩子。

1.4.4 优化
然而,简单地支持算法选项并不能直接在大规模集群上带来性能的提升。Bagua 的核心优势在于,为了追求极致化的性能,而实现算法和实现的联合优化。具体来讲,基于上述的通信层抽象,用户既可以方便得选择系统提供的各种算法组合从而获得性能提升,又能灵活得实现新的分布式 SGD 算法 —— Bagua 将自动为这一算法实现提供系统层优化。这些系统优化包含:
- 将通讯时间隐藏在计算时间中。
- 参数分桶及其内存管理。
- 分层化的通信实现。
想要强调的是,这些系统实现层面的优化是对于各种算法组合广泛适用,而非局限在某一特定的算法设置上。因此,所有的系统优化都可以被灵活的复用到各种算法实现中去,这在保证“端到端”的性能提升的同时,也为开发新的分布式算法提供了良好的平台。
1.5 流程图
我们使用官方号的图例做一下总结
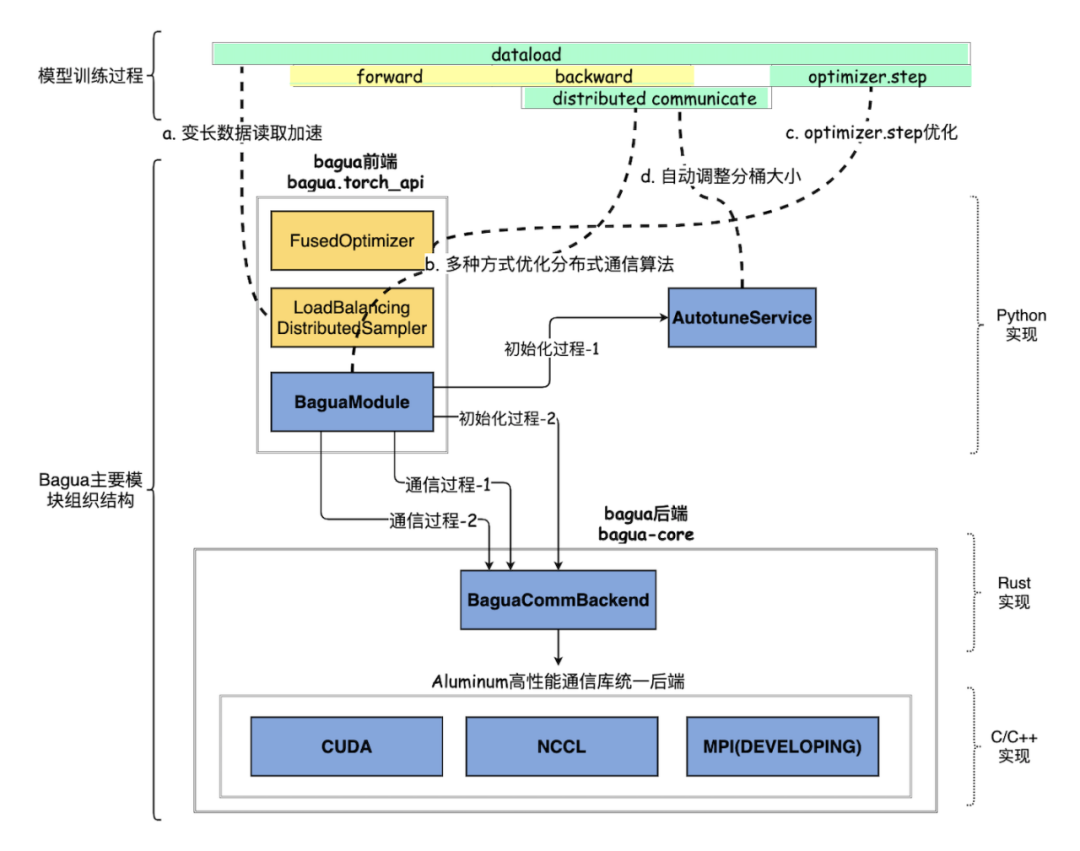
0x02 分析思路
通过官方文章我们可以发现对于分析学习来说有如下情况:
- 通信方面的优化实现是八卦项目的一大特点。
- 底层 Rust 语言笔者不熟悉。
- 通盘研究整体代码不现实。
因此我们决定以 中心化、异步通讯,分层化的通信实现 为中心,再结合几个特色实现来学习分析。本文学习负载均衡数据加载器。
0x03 Load Balanced Data Loader
在某些场景下当训练数据中样本的计算复杂度是不同的,比如在 NLP 和语音任务中每个样本的长度就不同。这时,使用八卦的负载均衡数据加载器可以大大提高分布式训练吞吐量,在这种情况下,worker 的工作负载是相似的。我们接下来就从实例入手,看看如何实现数据加载的负载均衡。
我们先看看负载均衡的需求,假如我们有两个模型副本进行数据并行,有如下数据,假如这些数据代表的是数据复杂度(会影响计算时间):
[ 7, 1, 11, 5, 10, 2, 9, 4, 6, 0, 8, 3]
那么第一个模型副本收到的数据为:[7,11,10,9,6, 8]。第二个模型副本收到的数据为:[1,5,2,4,0,3]。可以看出来两个模型在每个batch收到数据的复杂度不同,会造成负载不均衡。
+ 8 + 3
| |
| 6 | 0
| |
| 9 | 4
| |
batch 3 +-----------> | 10 | 2 <----------+ batch 3
| |
batch 2 +-----------> | 11 | 5 <----------+ batch 2
| |
batch 1 +-----------> v 7 v 1 <----------+ batch 1
+-------------------+ +-------------------+
| | | |
| worker 0 | | worker 1 |
| | | |
| | | |
+-------------------+ +-------------------+
理想状态应该是两个模型每个batch收到的数据复杂度都相仿,比如第一个模型收到 [1,3,5,7,9],第二个模型的数据是[2,4,6,8,10],在下图的输入下,可以看到每次batch数据复杂度相仿,从而达到负载均衡的效果:
+ +
| 9 | 10
| |
| 7 | 8
| |
batch 3 +-----------> | 5 | 6 <----------+ batch 3
| |
batch 2 +-----------> | 3 | 4 <----------+ batch 2
| |
batch 1 +-----------> v 1 v 2 <----------+ batch 1
+-------------------+ +-------------------+
| | | |
| worker 0 | | worker 1 |
| | | |
| | | |
+-------------------+ +-------------------+
3.1 使用
我们直接使用源码中的例子修改学习一下。
import torch
from load_balancing_data_loader import LoadBalancingDistributedSampler
from torch.utils.data import TensorDataset, DataLoader
def test_load_balancing_distributed_batch_sampler():
num_replicas = 2 # 分成两个副本
total_batch = 3
n = sum([i + 1 for i in range(total_batch)]) * num_replicas
dataset = TensorDataset(torch.randn(n, 2), torch.randperm(n))
sampler = LoadBalancingDistributedSampler(
dataset,
complexity_fn=lambda x: x[1],
num_replicas=num_replicas,
rank=0,
shuffle=True, # 需要shuffle
random_level=0.5, # 加入随机
)
dataloader = torch.utils.data.DataLoader(dataset, sampler=sampler)
cur_idx = 0
for i, data in enumerate(dataloader):
batch_size = data[0].shape[0]
cur_idx += batch_size * num_replicas
print(cur_idx)
test_load_balancing_distributed_batch_sampler()
因为此处代码十分绕,所以我们逐次解析。
3.2 生成数据集
首先是生成数据集部分。torch.randn(n, 2) 生成了随机张量,torch.randperm(n) 生成了 n 的随机排序。这里假定 n 是12。
# 生成了数据集
n = sum([i + 1 for i in range(total_batch)]) * num_replicas
dataset = TensorDataset(torch.randn(n, 2), torch.randperm(n))
TensorDataset 类似 zip 命令,生成了tuple列表。
dataset = {TensorDataset: 12}
tensors = {tuple: 2} (
0 = {Tensor: 12} tensor([[-1.5556, 0.6848],\n [ 2.0811, 1.5011],\n [ 0.7434, -0.4990],\n [-0.2706, 1.7227],\n [ 0.2179, 0.0622],\n [-0.3014, -0.6435],\n [-0.1773, -1.3405],\n [-1.8212, 0.3702],\n [-0.5526, -0.2077],\n [-1.6543, 0.3109],\n [ 0.3265, 0.5987],\n [-1.5566, 0.2854]])
1 = {Tensor: 12} tensor([ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3])
得出目前的TensorDataset如下 ,0 是实际数据,1 是数据复杂度,后续处理的目的就是按照数据复杂度对这些张量排序。我们可以设想下,最终排序应该就是一个复杂度均匀的排序结果。
+-----------------------------------------------------------------------------+
| TensorDataset |
| |
| 0 = {Tensor: 12} tensor([[-1.5556, 0.6848],...... |
| |
| 1 = {Tensor: 12} tensor([ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3]) |
| |
+-----------------------------------------------------------------------------+
3.3 初始化
我们来到了 LoadBalancingDistributedSampler 的初始化。
def __init__(
self,
dataset: Dataset,
complexity_fn: Callable[..., int],
num_replicas: Optional[int] = None,
rank: Optional[int] = None,
shuffle: bool = True,
seed: int = 0,
drop_last: bool = False,
random_level: float = 0,
) -> None:
if num_replicas is None:
num_replicas = dist.get_world_size()
if rank is None:
rank = dist.get_rank()
self.dataset = dataset
self.num_replicas = num_replicas
self.rank = rank
self.epoch = 0
self.drop_last = drop_last
# If the dataset length is evenly divisible by # of replicas, then there
# is no need to drop any data, since the dataset will be split equally.
dataset_len = len(self.dataset) # type: ignore
if self.drop_last and dataset_len % self.num_replicas != 0: # type: ignore
# Split to nearest available length that is evenly divisible.
# This is to ensure each rank receives the same amount of data when
# using this Sampler.
self.num_samples = math.ceil(
# `type:ignore` is required because Dataset cannot provide a default __len__
# see NOTE in pytorch/torch/utils/data/sampler.py
(dataset_len - self.num_replicas)
/ self.num_replicas
)
else:
self.num_samples = math.ceil(dataset_len / self.num_replicas) # type: ignore
self.total_size = self.num_samples * self.num_replicas
self.shuffle = shuffle
self.seed = seed
"""
此时变量为
self = {LoadBalancingDistributedSampler: 6}
dataset = {TensorDataset: 12} <torch.utils.data.dataset.TensorDataset object at 0x7ff7385aecf8>
drop_last = {bool} False
epoch = {int} 0
num_replicas = {int} 2
num_samples = {int} 6
rank = {int} 0
seed = {int} 0
shuffle = {bool} True
total_size = {int} 12
"""
# 以下是与PyTorch原生的主要不同之处
self.item_complexity_map = dict()
for item_index in range(dataset_len):
# 每一个item都有一个complexity
self.item_complexity_map[item_index] = complexity_fn(
self.dataset[item_index]
)
"""
complexity_fn 是选取 tuple 的第二个元素作为复杂度,我们回忆一下数据集的复杂度
{Tensor: 12} tensor([ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3])
所以得到了复杂度map如下:
item_complexity_map = {dict: 12} {0: tensor(7), 1: tensor(8), 2: tensor(11), 3: tensor(4), 4: tensor(5), 5: tensor(2), 6: tensor(9), 7: tensor(10), 8: tensor(0), 9: tensor(6), 10: tensor(1), 11: tensor(3)}
0 = {Tensor} tensor(7) # 第 0 个元素复杂度是 7
1 = {Tensor} tensor(8) # 第 1 个元素复杂度是 8
2 = {Tensor} tensor(11)
3 = {Tensor} tensor(4)
4 = {Tensor} tensor(5)
5 = {Tensor} tensor(2)
6 = {Tensor} tensor(9)
7 = {Tensor} tensor(10)
8 = {Tensor} tensor(0)
9 = {Tensor} tensor(6)
10 = {Tensor} tensor(1)
11 = {Tensor} tensor(3)
"""
# 按照复杂度排序
self.ordered_item_complexity_map = OrderedDict(
sorted(self.item_complexity_map.items(), key=lambda t: t[1])
)
"""
排序之后如下:
ordered_item_complexity_map = {OrderedDict: 12} OrderedDict([(8, tensor(0)), (10, tensor(1)), (5, tensor(2)), (11, tensor(3)), (3, tensor(4)), (4, tensor(5)), (9, tensor(6)), (0, tensor(7)), (1, tensor(8)), (6, tensor(9)), (7, tensor(10)), (2, tensor(11))])
8 = {Tensor} tensor(0) 第8个元素复杂度最低,是0
10 = {Tensor} tensor(1) # 第10个元素复杂度次低,是1
5 = {Tensor} tensor(2)
11 = {Tensor} tensor(3)
3 = {Tensor} tensor(4)
4 = {Tensor} tensor(5)
9 = {Tensor} tensor(6)
0 = {Tensor} tensor(7)
1 = {Tensor} tensor(8)
6 = {Tensor} tensor(9)
7 = {Tensor} tensor(10)
2 = {Tensor} tensor(11)
"""
max_complexity = max(self.item_complexity_map.values()) # 11
min_complexity = min(self.item_complexity_map.values()) # 0
self.random_number = int((max_complexity - min_complexity) * random_level + 1) # 6
# random_number = {int} 1
拓展如下:
- TensorDataset ,0 = ... 是实际数据,1 = ... 是数据复杂度,后续就是按照复杂度排序,而且所有排序或者打乱都没有对原始数据进行移动,而是通过额外空间完成。
- 初始化内部会对复杂度进行排序,
- item_complexity_map 是得到每个元素的原始复杂度,比如 0: 7 表示第 0 个元素复杂度是 7。
- ordered_item_complexity_map 就是排序之后的结构,其中 (8, 0) 表示第8个元素复杂度最低,是0,整个map是升序排列。
TensorDataset 的逻辑图拓展如下,现在数据集 ordered_item_complexity_map 之中按照复杂度从低到高进行排序了。
+-----------------------------------------------------------------------------+
| TensorDataset |
| |
| 0 = {Tensor: 12} tensor([[-1.5556, 0.6848],...... |
| |
| 1 = {Tensor: 12} tensor([ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3]) |
| |
+-------------------------------------------+---------------------------------+
|
|
v
+-------------------------------------------+------------------------------------------+
| LoadBalancingDistributedSampler.__init__ |
| |
| |
| item_complexity_map = {dict: 12} {0: 7, 1: 8, 2: 11, 3: 4, 4: 5, 5: 2, |
| |
| 6: 9, 7: 10, 8: 0, 9: 6, 10: 1, 11: 3} |
| + |
| | |
| | sorted |
| | |
| v |
| ordered_item_complexity_map = {OrderedDict: 12} [(8, 0), (10, 1), (5, 2), (11, 3), |
| |
| (3, 4), (4, 5), (9, 6), (0, 7), (1, 8), (6, 9), (7, 10), (2, 11)] |
| |
+--------------------------------------------------------------------------------------+
3.4 使用
示例代码之中接下来是使用数据:
dataloader = torch.utils.data.DataLoader(dataset, sampler=sampler)
cur_idx = 0
for i, data in enumerate(dataloader):
batch_size = data[0].shape[0]
cur_idx += batch_size * num_replicas
print(cur_idx)
3.4.1 获取数据
我们接下来看看如何获取数据,就是如何从loader拿到sample。
- 首先会调用 shuffle_chunks 来打乱数据。
- 然后得到自己rank对应的index。
def __iter__(self) -> Iterator:
index_chunks, chunk_indices = self.shuffle_chunks() # 打乱数据
# subsample
indices = [index_chunks[i][self.rank] for i in chunk_indices] # 用 rank来提取数据
"""
得到数据如下:
chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3] 把 index_chunks 顺序打乱,chunk_indices 是打乱之后的结果
index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] 均匀分成两组
indices = {list: 6} [8, 7, 6, 5, 4, 0] 得到自己rank对应的index
"""
return iter(indices)
3.4.2 shuffle
我们看看shuffle 具体代码如下,这里最终要分成 6 = 12(数据数目) / 2( num_replicas ) 组数据。
def shuffle_chunks(self):
def chunks_wrap_padding(lst, n):
"""Yield successive n-sized chunks from lst."""
num_chunks = max(1, self.num_samples)
num_elements = num_chunks * n
current_lst = []
for i in range(num_elements):
current_lst.append(lst[i % len(lst)])
if len(current_lst) == n:
yield current_lst
current_lst = []
if self.shuffle: # 需要再次打乱
# deterministically shuffle based on epoch and seed
g = torch.Generator()
g.manual_seed(self.seed + self.epoch)
if self.random_number > 0:
# 这里的打乱机制很巧妙,就是随机再生成复杂度,然后加到原先复杂度map上
item_complexity_map = self.item_complexity_map.copy() # 原来map做个拷贝
complexity_random_ints = torch.randint( # 新生成了一些复杂度变化值
self.random_number, (len(item_complexity_map),), generator=g
).tolist()
"""
complexity_random_ints = {list: 12} [2, 3, 5, 0, 1, 3, 1, 1, 1, 3, 5, 2]
item_complexity_map = {dict: 12} {0: tensor(7), 1: tensor(8), 2: tensor(11), 3: tensor(4), 4: tensor(5), 5: tensor(2), 6: tensor(9), 7: tensor(10), 8: tensor(0), 9: tensor(6), 10: tensor(1), 11: tensor(3)}
"""
# 原来复杂度map + 复杂度变化值
for k, v in zip(item_complexity_map, complexity_random_ints):
item_complexity_map[k] += v
"""
生成新的复杂度
item_complexity_map = {0: tensor(9), 1: tensor(11), 2: tensor(16), 3: tensor(4), 4: tensor(6), 5: tensor(5), 6: tensor(10), 7: tensor(11), 8: tensor(1), 9: tensor(9), 10: tensor(6), 11: tensor(5)}
"""
# 再次对新复杂度排序
ordered_item_complexity_map = OrderedDict(
sorted(item_complexity_map.items(), key=lambda t: t[1])
)
"""
ordered_item_complexity_map = {OrderedDict: 12} OrderedDict([(8, tensor(1)), (3, tensor(4)), (5, tensor(5)), (11, tensor(5)), (4, tensor(6)), (10, tensor(6)), (0, tensor(9)), (9, tensor(9)), (6, tensor(10)), (1, tensor(11)), (7, tensor(11)), (2, tensor(16))])
8 = {Tensor} tensor(1)
3 = {Tensor} tensor(4)
5 = {Tensor} tensor(5)
11 = {Tensor} tensor(5)
4 = {Tensor} tensor(6)
10 = {Tensor} tensor(6)
0 = {Tensor} tensor(9)
9 = {Tensor} tensor(9)
6 = {Tensor} tensor(10)
1 = {Tensor} tensor(11)
7 = {Tensor} tensor(11)
2 = {Tensor} tensor(16)
__len__ = {int} 12
"""
else:
ordered_item_complexity_map = self.ordered_item_complexity_map
index_chunks = list( # 按照 num_replicas 进行分片
chunks_wrap_padding(
list(ordered_item_complexity_map.keys()), self.num_replicas
)
)
"""
被均匀分配成两组,每组中两个元素的复杂度接近
index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]]
0 = {list: 2} [8, 3]
1 = {list: 2} [5, 11]
2 = {list: 2} [4, 10]
3 = {list: 2} [0, 9]
4 = {list: 2} [6, 1]
5 = {list: 2} [7, 2]
__len__ = {int} 6
"""
# 再次打乱 index_chunks
chunk_indices = torch.randperm(len(index_chunks), generator=g).tolist() # type: ignore
"""
chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3]
"""
else:
index_chunks = list(
chunks_wrap_padding(
list(self.ordered_item_complexity_map.keys()), self.num_replicas
)
)
chunk_indices = list(range(len(index_chunks))) # type: ignore
if not self.drop_last:
# add extra samples to make it evenly divisible
padding_size = self.num_samples - len(chunk_indices)
if padding_size <= len(chunk_indices):
chunk_indices += chunk_indices[:padding_size]
else:
chunk_indices += (
chunk_indices * math.ceil(padding_size / len(chunk_indices))
)[:padding_size]
else:
# remove tail of data to make it evenly divisible.
chunk_indices = chunk_indices[: self.num_samples]
assert len(chunk_indices) == self.num_samples
return index_chunks, chunk_indices
总体拓展如下:
- TensorDataset ,0 = ... 是实际数据,1 = ... 是数据复杂度,后续就是按照复杂度排序:
-
LoadBalancingDistributedSampler.__init__初始化内部会对复杂度进行排序,- item_complexity_map 是得到每个元素的复杂度,比如 0: 7 表示第 0 个元素复杂度是 7。
- ordered_item_complexity_map 就是按照复杂度排序之后的结构,其中 (8, 0) 表示第8个元素复杂度最低,是0。
- shuffle_chunks 内部继续处理,这里的打乱机制很巧妙,没有移动数据,而是随机再生成复杂度,然后加到原先复杂度map上,这样就打乱了。
- complexity_random_ints 新生成了一些复杂度变化值。
- item_complexity_map 把原来map做个拷贝。
- item_complexity_map 继续操作,即:新复杂度 = 原来复杂度map + 复杂度变化值。
- ordered_item_complexity_map 对新复杂度排序。
- 对 ordered_item_complexity_map 按照 num_replicas 进行分片,得到 index_chunks,ordered_item_complexity_map 被均匀分配成六组,每组中两个元素的复杂度接近。
- 然后再次打乱 index_chunks,得到 chunk_indices,就是为了把index顺序打乱而已。
+--------------------------------------------------------------------------------------+
| TensorDataset |
| |
| 0 = {Tensor: 12} tensor([[-1.5556, 0.6848],...... |
| |
| 1 = {Tensor: 12} tensor([ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3]) |
| |
+-------------------------------------------+------------------------------------------+
|
|
v
+-------------------------------------------+------------------------------------------+
| LoadBalancingDistributedSampler.__init__ |
| |
| |
| item_complexity_map = {dict: 12} {0: 7, 1: 8, 2: 11, 3: 4, 4: 5, 5: 2, |
| |
| 6: 9, 7: 10, 8: 0, 9: 6, 10: 1, 11: 3} |
| + |
| | |
| | sorted |
| | |
| v |
| ordered_item_complexity_map = {OrderedDict: 12} [(8, 0), (10, 1), (5, 2), (11, 3), |
| |
| (3, 4), (4, 5), (9, 6), (0, 7), (1, 8), (6, 9), (7, 10), (2, 11)] |
| |
+-------------------------------------------+------------------------------------------+
|
|
v
+-------------------------------------------+------------------------------------------+
| __iter__ |
| |
+-------------------------------------------+------------------------------------------+
|
|
v
+-------------------------------------------+------------------------------------------+
| |
| shuffle_chunks() |
| |
| |
| complexity_random_ints = {list: 12} [2, 3, 5, 0, 1, 3, 1, 1, 1, 3, 5, 2] |
| |
| |
| |
| item_complexity_map = {0: 9, 1: 11, 2: 16, 3: 4, 4: 6, 5: 5, 6: 10, 7: 11, 8: 1, |
| |
| 9: 9, 10: 6, 11: 5} |
| |
| |
| |
| ordered_item_complexity_map = {OrderedDict: 12} [(8, 1), (3, 4), (5, 5), (11, 5), |
| |
| (4, 6), (10, 6), (0, 9), (9, 9), |
| |
| (6, 10), (1, 11), (7, 11), (2, 16)]) |
| |
| + |
| | |
| | |
| v |
| |
| index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] |
| |
| |
| chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3] |
| |
| |
+--------------------------------------------------------------------------------------+
3.4.3 梳理
shuffle 细化
看到这里读者可能有点晕,所以我们需要具体梳理一下。
ordered_item_complexity_map 就是按照复杂度排序之后的结构,其中 (8, 0) 表示第8个元素复杂度最低,是0。ordered_item_complexity_map 拥有 12个元素,按照两个副本分配,所以 ordered_item_complexity_map 应该被均匀分配成六组,每组中两个元素的复杂度接近。
index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] 是最终的结果,这里[8, 3]是一组,复杂度接近,[5, 11]是一组,复杂度接近,比如结合 ordered_item_complexity_map 来看:
-
(8, 1), (3, 4) 就是说,第 8 个元素复杂度是1,第3个元素复杂度是4,所以 index 8,index 3 被分成一组。
-
(5, 5), (11, 5) 就是说,第 5 个元素复杂度是5,第11个元素复杂度是5,所以 index 5,index 11 被分成一组。
shuffle_chunks 的演示如下:
+--------------------------------------------------------------------------------------+
| shuffle_chunks |
| |
| |
| +--------------+ +---------------+ |
| ordered_item_complexity_map = [ +--+(8, 1), (3, 4)| +-+(5, 5), (11, 5)| |
| | +--------------+ | +---------------+ |
| | | |
| | +---------------+ | +---------------+ |
| +-------+(4, 6), (10, 6)| | |(0, 9), (9, 9) +-------+ |
| | | +---------------+ | +---------------+ | |
| | | | | |
| | | +----------------+ | +----------------+ | |
| | | |(6, 10), (1, 11)| | |(7, 11), (2, 16)| ] | |
| | | +-------------+--+ | +----------+-----+ | |
| | | | | | | |
| +------------------+ +-------------+ +----+ | |
| | | | | | | |
| | +------------+ +---------------------+ |
| | | | | | | |
| v v v v v v |
| index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] |
| |
| + |
| | |
| | |
| v |
| |
| chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3] |
| |
+--------------------------------------------------------------------------------------+
二次打乱
我们结合原始数据再来分析,先回头看看 获取数据。
def __iter__(self) -> Iterator:
index_chunks, chunk_indices = self.shuffle_chunks()
# subsample
indices = [index_chunks[i][self.rank] for i in chunk_indices]
"""
得到数据如下:
chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3] 把 index_chunks 顺序打乱
index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] 均匀分成两组
indices = {list: 6} [8, 7, 6, 5, 4, 0] 得到自己rank对应的index
"""
assert len(indices) == self.num_samples
return iter(indices)
原始数据为 :[ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3],后续会按照原始数据的index 来排序。
按照复杂度排序/shuffle之后,rank 0 就是 [8, 5, 4, 0, 6, 7]。rank 1 就是 [3, 11, 10, 9, 1, 2]。
rank 0 和 rank 1 的batch 是 [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] ,两两一组。
但是,还需要再次打乱顺序,因为目前这个batch是按照复杂度从小到大排序,这样会影响训练效果,所以需要打乱这个顺序。所以就按照 chunk_indices [0, 5, 4, 1, 2, 3] 这个顺序来打乱。
打乱之后的顺序是:[[8, 3], [7, 2], [6, 1], [5, 11], [4, 10], [0, 9]]。
-
假如本worker 是 rank 0,则会获取 index_chunks 这六组数据中和自己对应的,得到 [8, 7, 6, 5, 4, 0]。
-
假如本worker rank 1,则是 [3,2,1,11,10,9]。注意,这些还都是原始数据的index。
具体演示如下图(这里只给出 rank 0 的效果):
+--------------------------------------------------------------------------------------+
| shuffle_chunks |
| |
| +--------------+ +---------------+ |
| ordered_item_complexity_map = [ +--+(8, 1), (3, 4)| +-+(5, 5), (11, 5)| |
| | +--------------+ | +---------------+ |
| | | |
| | +---------------+ | +---------------+ |
| +------+(4, 6), (10, 6)| | |(0, 9), (9, 9) +------+ |
| | | +---------------+ | +---------------+ | |
| | | | | |
| | | +----------------+ | +----------------+ | |
| | | |(6, 10), (1, 11)| | |(7, 11), (2, 16)| ] | |
| | | +-------------+--+ | +----------+-----+ | |
| | | | | | | |
| +-----------------+ +-------------+ +----+ | |
| | | | | | | |
| | +------------+ +--------------------+ |
| | | | | | | |
| v v v v v v |
| index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] |
| + |
| | |
| | |
| v |
| chunk_indices = {list: 6} [0, 5, 4, 1, 2, 3] |
| |
+--------------------------------------+-----------------------------------------------+
|
|
v
+--------------------------------------------------------------------------------------+
| __iter__ |
| 0 1 2 3 4 5 |
| index_chunks = {list: 6} [[8, 3], [5, 11], [4, 10], [0, 9], [6, 1], [7, 2]] |
| + + + + + + |
| | | | | | | |
| +----+ +-----+ | +-----+ | | |
| | | | | | | |
| | | | | | | |
| v v v v | | |
| indices = {list: 6} [8, 7, 6, 5, 4, 0] | | |
| ^ ^ | | |
| | | | | |
| | +----------------------+ | |
| | | |
| +---------------------------------+ |
| |
+--------------------------------------------------------------------------------------+
最终效果
我们看看最终效果是什么:
-
原始数据为 :[ 7, 8, 11, 4, 5, 2, 9, 10, 0, 6, 1, 3]。
-
最终shuffle/二次打乱之后的数据为:rank 0 是 [8, 7, 6, 5, 4, 0],rank 1 则是 [3,2,1,11,10,9]。这里数值是原始数据的index。
-
最终结果是:
- batch如下,rank 0 和 rank 1 的batch 是 [[8, 3], [7, 2], [6, 1], [5, 11], [4, 10], [0, 9]],两两一组。这里数值是原始数据的index。
- rank 0 的数据是 [0, 10, 9, 2, 5, 7],rank 1的数据是[4, 11, 7, 3, 1, 6],这里数值就是原始数据的数值了。
具体如下图,可以看到,因为过程之中引入了随机值,所以不是理想均衡状态,但已经比较均衡了:
+ 7 + 6
| |
| 5 | 1
| |
| 2 | 3
| |
batch 3 +-----------> | 9 | 7 <----------+ batch 3
| |
batch 2 +-----------> | 10 | 11 <----------+ batch 2
| |
batch 1 +-----------> v 0 v 4 <----------+ batch 1
+-------------------+ +-------------------+
| | | |
| worker 0 | | worker 1 |
| | | |
| | | |
+-------------------+ +-------------------+
0xFF 参考
快手八卦!突破 TensorFlow、PyTorch 并行瓶颈的开源分布式训练框架来了!
https://arxiv.org/pdf/2107.01499.pdf
[1] Dean, Jeffrey, Greg S. Corrado, Rajat Monga, Kai Chen, Matthieu Devin, Quoc V. Le, Mark Z. Mao et al. “Large scale distributed deep networks.” (2012).
[2] Zhengyuan Zhou, Panayotis Mertikopoulos, Nicholas Bambos, Peter Glynn, Yinyu Ye, Li-Jia Li, and Li Fei-Fei. 2018. Distributed asynchronous optimization with unbounded delays: How slow can you go?. In International Conference on Machine Learning. PMLR, 5970–5979.
[3] DanAlistarh, DemjanGrubic, JerryLi, RyotaTomioka, and MilanVojnovic. 2016. QSGD: Communication-efficient SGD via gradient quantization and encoding. arXiv preprint arXiv:1610.02132 (2016).
[4] Dan Alistarh, Torsten Hoefler, Mikael Johansson, Sarit Khirirat, Nikola Konstanti- nov, and Cédric Renggli. 2018. The convergence of sparsified gradient methods. In Proceedings of the 32nd International Conference on Neural Information Processing Systems. 5977–5987.
[5] Anastasia Koloskova, Sebastian Stich, and Martin Jaggi. 2019. Decentralized stochastic optimization and gossip algorithms with compressed communication. In International Conference on Machine Learning. PMLR, 3478–3487.
[6] Xiangru Lian, Ce Zhang, Huan Zhang, Cho-Jui Hsieh, Wei Zhang, and Ji Liu. 2017. Can decentralized algorithms outperform centralized algorithms? a case study for decentralized parallel stochastic gradient descent. In Proceedings of the 31st International Conference on Neural Information Processing Systems. 5336–5346.
[7] Christopher De Sa, Matthew Feldman, Christopher Ré, and Kunle Olukotun. 2017. Understanding and optimizing asynchronous low-precision stochastic gradient descent. In Proceedings of the 44th Annual International Symposium on Computer Architecture. 561–574.
[8] Xiangru Lian, Wei Zhang, Ce Zhang, and Ji Liu. 2018. Asynchronous decentral- ized parallel stochastic gradient descent. In International Conference on Machine Learning. PMLR, 3043–3052.
[9] Hanlin Tang, Shaoduo Gan, Ce Zhang, Tong Zhang, and Ji Liu. 2018. Com- munication compression for decentralized training. In Proceedings of the 32nd International Conference on Neural Information Processing Systems. 7663–7673.
[10] Ji Liu, Ce Zhang, et al. 2020. Distributed Learning Systems with First-Order Methods. Foundations and Trends® in Databases 9, 1 (2020), 1–100.![]
