引子
你某天在洛谷里刷题,梦想着有一天AK IOI(@DXR),这时,你看到了一个橙题,但是AC率仅仅只有 \(\frac{1}{3}\) ,你寻思着一道橙题会有多难,于是决定写这道题
题目
-
对于一个递归函数\(w(a,b,c)\)
-
如果\(a \le 0\) or \(b \le 0\) or \(c \le 0\)就返回值\(1\).
-
如果\(a > 20\) or \(b > 20\) or \(c > 20\)就返回\(w(20,20,20)\)
-
如果\(a < b\)并且\(b < c\) 就返回\(w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)\)
-
其它的情况就返回\(w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)\)
你不屑的把所有的公式都打上去
#include<cstdio>
#include<iostream>
using namespace std;
inline long long w(long long a,long long b,long long c)
{
if(a<=0||b<=0||c<=0) return 1;
else if(a>20||b>20||c>20) return w(20,20,20);
else if(a<b&&b<c) return w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
else return w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
return w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
}
int main()
{
long long a,b,c;
for(register int i=1; ;i++)
{
scanf("%lld%lld%lld",&a,&b,&c);
if(a==-1&&b==-1&&c==-1) break;
printf("w(%lld, %lld, %lld) = ",a,b,c);
printf("%lld\n",w(a,b,c));
}
return 0;
}
然后看到的会是
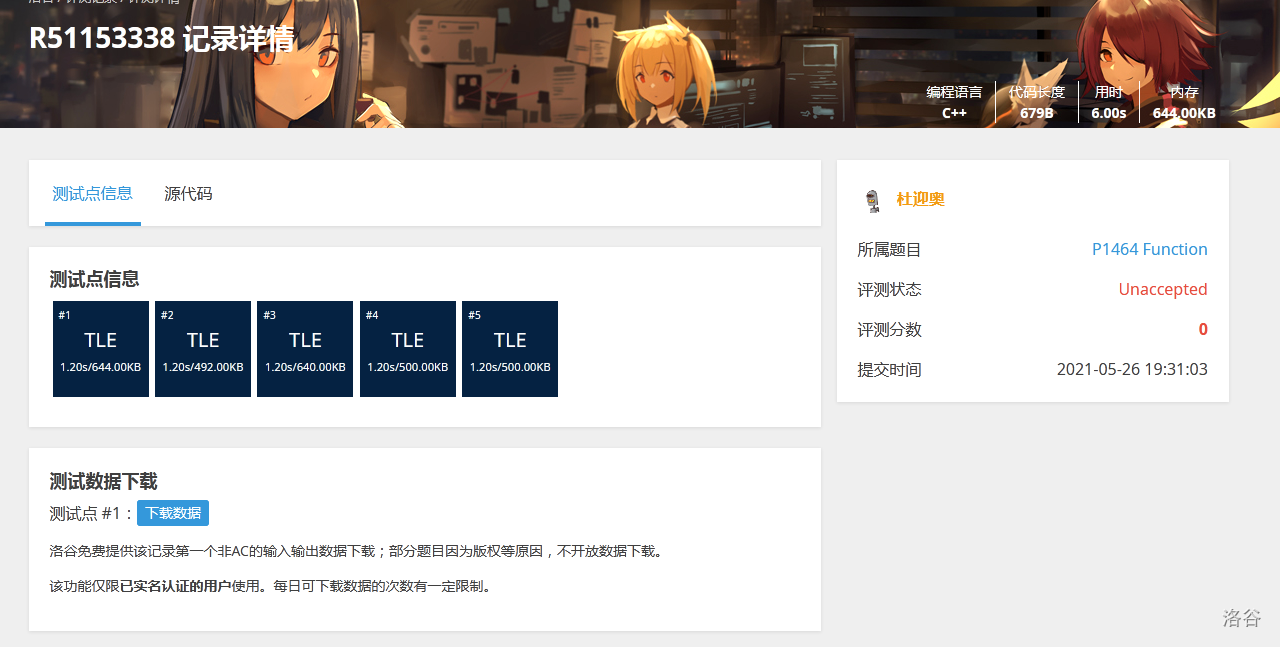
然后你陷入了沉思...

正题
很显然,我们打的这个程序十分的垃圾,当输入50,50,50的数据时,就会瞬间爆炸,全程TLE,比赛时是绝对不能出现这种情况的
那么我们如何解决这种问题呢
这个题目全都是递归公式,也许我们可以在这上面下手......
你用你聪明的大脑想到,有时候递归的a,b,c会是和之前某个时候相等的,我们可以开一个数组存储一下......
然后......
#include<cstdio>
#include<iostream>
using namespace std;
long long m[25][25][25];
inline long long w(long long a,long long b,long long c)
{
if(a<=0||b<=0||c<=0) return 1;
else if(m[a][b][c]!=0) return m[a][b][c];
else if(a>20||b>20||c>20) m[a][b][c]=w(20,20,20);
else if(a<b&&b<c) m[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
else m[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
return m[a][b][c];
}
int main()
{
long long a,b,c;
for(register int i=1; ;i++)
{
scanf("%lld%lld%lld",&a,&b,&c);
if(a==-1&&b==-1&&c==-1) break;
printf("w(%lld, %lld, %lld) = ",a,b,c);
printf("%lld\n",w(a,b,c));
}
return 0;
}
光荣\({RE}\)

但是这个时候,我们的时间复杂度会下降不少,起码当数据为 \(50,50,50\) 时,我们不会爆炸,RE的原因只是因为题目范围,经过一番 玄学 分析之后,我们发现当 \(a,b,c\) 中任意一个值大于 \(20\) 时,返回值都是一样的,我们只需要加个判断即可
#include<cstdio>
#include<iostream>
using namespace std;
long long m[25][25][25];
inline long long w(long long a,long long b,long long c)
{
if(a<=0||b<=0||c<=0) return 1;
else if(m[a][b][c]!=0) return m[a][b][c];
else if(a>20||b>20||c>20) m[a][b][c]=w(20,20,20);
else if(a<b&&b<c) m[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
else m[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
return m[a][b][c];
}
int main()
{
long long a,b,c;
for(register int i=1; ;i++)
{
scanf("%lld%lld%lld",&a,&b,&c);
if(a==-1&&b==-1&&c==-1) break;
printf("w(%lld, %lld, %lld) = ",a,b,c);
if(a>20) a=21;
if(b>20) b=21;
if(c>20) c=21;
printf("%lld\n",w(a,b,c));
}
return 0;
}
讲解
看到这里,我相信大家对记忆化搜索已经有一个基本了解了,它就是一个换装玩角色扮演的DFS,伪装成高级的样子和DP混在一起(这点我后面会讲解)
我们结合另一道题理解
看完题目,你会想到一个个枚举每一个点,进行大爆搜,如果你是这么想的,请重新回到文章篇头再看一遍记忆化搜索的思路是什么,因为这题实际是记忆化搜索
对于每一个点,我们进行一次搜索,找出它滑雪距离的最大值,存储下来,方便下一次使用
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int n,m,a[201][201],s[201][201],ans;
int dfs(int x,int y){
if(s[x][y])return s[x][y];//记忆化搜索
s[x][y]=1;//题目中答案是有包含这个点的
for(int i=0;i<4;i++)
{ int xx=dx[i]+x;
int yy=dy[i]+y;//四个方向
if(xx>0&&yy>0&&xx<=n&&yy<=m&&a[x][y]>a[xx][yy]){
dfs(xx,yy);
s[x][y]=max(s[x][y],s[xx][yy]+1);
}
}
return s[x][y];
}
int main()
{
scanf("%d%d",&n,&m);//同题目的R,C
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)//找从每个出发的最长距离
for(int j=1;j<=m;j++)
ans=max(ans,dfs(i,j));//取最大值
printf("%d",ans);
return 0;
}
然后,我们发现一个神奇的地方......
s[x][y]=max(s[x][y],s[xx][yy]+1)
这行代码,是不是特别熟悉?
没错,这就是一个状态转移方程,所以我说记忆化搜索就是玩角色扮演的DFS,装作DP的亚子,所以实际上这题也可以用DP来解,和上面的代码也差不太多
总结
再仔细观察一下咱的代码,发现记忆化搜索中的DFS函数几乎不需要外部变量( 自力更生),这也是记忆化搜索的特点之一
所以我们得出记忆化搜索的总结
- 不依赖任何 外部变量
- 答案以返回值的形式存在,而不能以参数的形式存在(就是不能将 dfs 定义成 \(dfs( pos , tleft , nowans )\),这里面的 \(nowans\) 不符合要求)。
- 对于相同一组参数,dfs 返回值总是相同的
例题
既然说记忆化搜索就是玩角色扮演的DFS,装作DP,那么几乎所有的DP,都可以用记忆化求解(好耶)
DP Code
#include<stdio.h>
int max(int a,int b)
{
if (a>b) return a;
else return b;
}
int main()
{
int f[1000]={0},c[1000],w[1000];
int n,v,i,j;
scanf("%d%d",&v,&n);
for(i=1;i<=n;i++)scanf("%d%d",&c[i],&w[i]);
for(i=1;i<=n;i++)
for(j=v;j>=c[i];j--)
{
f[j]=max(f[j],f[j-c[i]]+w[i]);
}
printf("%d ",f[v]);
return 0;
}
记忆化 Code
int n,t;
int tcost[103],mget[103];
int mem[103][1003];
int dfs(int pos,int tleft){
if( mem[pos][tleft] != -1 ) return mem[pos][tleft];
if(pos == n+1)
return mem[pos][tleft] = 0;
int dfs1,dfs2 = -INF;
dfs1 = dfs(pos+1,tleft);
if( tleft >= tcost[pos] )
dfs2 = dfs(pos+1,tleft-tcost[pos]) + mget[pos];
return mem[pos][tleft] = max(dfs1,dfs2);
}
int main(){
memset(mem,-1,sizeof(mem));
cin >> t >> n;
for(int i = 1;i <= n;i++)
cin >> tcost[i] >> mget[i];
cout << dfs(1,t) << endl;
return 0;
}
