
什么是基数估算
HyperLogLog 是一种基数估算算法。所谓基数估算,就是估算在一批数据中,不重复元素的个数有多少。
从数学上来说,基数估计这个问题的详细描述是:对于一个数据流 {x1,x2,...,xs} 而言,它可能存在重复的元素,用 n 来表示这个数据流的不同元素的个数,并且这个集合可以表示为{e1,...,en}。目标是:使用 m 这个量级的存储单位,可以得到 n 的估计值,其中 m<<n 。并且估计值和实际值 n 的误差是可以控制的。
对于上面这个问题,如果是想得到精确的基数,可以使用字典(dictionary)这一个数据结构。对于新来的元素,可以查看它是否属于这个字典;如果属于这个字典,则整体计数保持不变;如果不属于这个字典,则先把这个元素添加进字典,然后把整体计数增加一。当遍历了这个数据流之后,得到的整体计数就是这个数据流的基数了。
这种算法虽然精准度很高,但是使用的空间复杂度却很高。那么是否存在一些近似的方法,可以估算出数据流的基数呢?HyperLogLog 就是这样一种算法,既可以使用较低的空间复杂度,最后估算出的结果误差又是可以接受的。
HyperLogLog 算法简介
HyperLogLog 算法的基本思想来自伯努利过程。
伯努利过程就是一个抛硬币实验的过程。抛一枚正常硬币,落地可能是正面,也可能是反面,二者的概率都是 1/2 。伯努利过程就是一直抛硬币,直到落地时出现正面位置,并记录下抛掷次数k。比如说,抛一次硬币就出现正面了,此时 k 为 1; 第一次抛硬币是反面,则继续抛,直到第三次才出现正面,此时 k 为 3。
那么如何通过伯努利过程来估算抛了多少次硬币呢?还是假设 1 代表抛出正面,0 代表反面。连续出现两次 0 的序列应该为“001”,那么它出现的概率应该是三个二分之一相乘,即八分之一。那么可以估计大概抛了 8 次硬币。
HyperLogLog 原理思路是通过给定 n 个的元素集合,记录集合中数字的比特串第一个1出现位置的最大值k,也可以理解为统计二进制低位连续为零(前导零)的最大个数。通过k值可以估算集合中不重复元素的数量m,m近似等于 2^k。
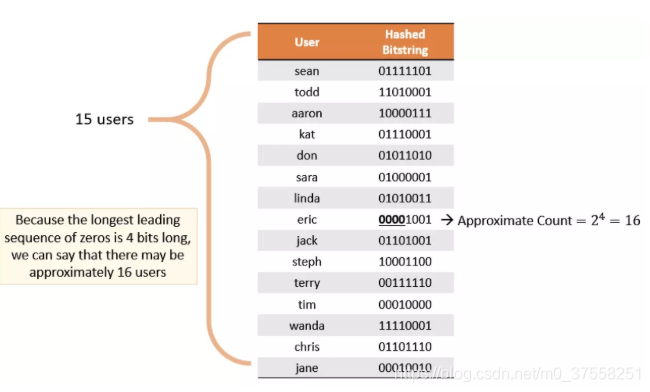
如上图所示,给定一定数量的用户,通过 Hash 算法得到一串 Bitstring,记录其中最大连续零位的计数为 4,User 的不重复个数为 2 ^ 4 = 16。
1. 分桶优化
HyperLogLog 的基本思想是利用集合中数字的比特串第一个 1 出现位置的最大值来预估整体基数,但是这种预估方法存在较大误差,为了改善误差情况,HyperLogLog中引入分桶平均的概念,计算 m 个桶的调和平均值。下面公式中的const是一个修正常量。
Redis 中 HyperLogLog 一共分了 2^14 个桶,也就是 16384 个桶。每个桶中是一个 6 bit 的数组,如下图所示。
HyperLogLog 将上文所说的 64 位比特串的低 14 位单独拿出,它的值就对应桶的序号,然后将剩下 50 位中第一次出现 1 的位置值设置到桶中。50位中出现1的位置值最大为50,所以每个桶中的 6 位数组正好可以表示该值。
在设置前,要设置进桶的值是否大于桶中的旧值,如果大于才进行设置,否则不进行设置。示例如下图所示。
在计算近似基数时,就分别计算每个桶中的值,带入到上文将的 DV 公式中,进行调和平均和结果修正,就能得到估算的基数值。
Redis 中的 HyperLogLog
Redis 提供了 PFADD 、 PFCOUNT 和 PFMERGE 三个命令来供用户使用 HyperLogLog。
# 用于向 HyperLogLog 添加元素
# 如果 HyperLogLog 估计的近似基数在 PFADD 命令执行之后出现了变化, 那么命令返回 1 , 否则返回 0
# 如果命令执行时给定的键不存在, 那么程序将先创建一个空的 HyperLogLog 结构, 然后再执行命令
pfadd key value1 [value2 value3]
# PFCOUNT 命令会给出 HyperLogLog 包含的近似基数
# 在计算出基数后, PFCOUNT 会将值存储在 HyperLogLog 中进行缓存,知道下次 PFADD 执行成功前,就都不需要再次进行基数的计算。
pfcount key
# PFMERGE 将多个 HyperLogLog 合并为一个 HyperLogLog , 合并后的 HyperLogLog 的基数接近于所有输入 HyperLogLog 的并集基数。
pfmerge destkey key1 key2 [...keyn]
应用场景
HyperLogLog 主要的应用场景就是进行基数统计。这个问题的应用场景其实是十分广泛的。例如:对于 Google 主页面而言,同一个账户可能会访问 Google 主页面多次。于是,在诸多的访问流水中,如何计算出 Google 主页面每天被多少个不同的账户访问过就是一个重要的问题。那么对于 Google 这种访问量巨大的网页而言,其实统计出有十亿 的访问量或者十亿零十万的访问量其实是没有太多的区别的,因此,在这种业务场景下,为了节省成本,其实可以只计算出一个大概的值,而没有必要计算出精准的值。
对于上面的场景,可以使用HashMap、BitMap和HyperLogLog 来解决。对于这三种解决方案,这边做下对比:
-
HashMap:算法简单,统计精度高,对于少量数据建议使用,但是对于大量的数据会占用很大内存空间; -
BitMap:位图算法,具体内容可以参考我的这篇文章,统计精度高,虽然内存占用要比HashMap少,但是对于大量数据还是会占用较大内存; -
HyperLogLog:存在一定误差,占用内存少,稳定占用 12k 左右内存,可以统计 2^64 个元素,对于上面举例的应用场景,建议使用。
